目录
- 本文异或算法聊起,循序渐进推导了对称加密算法的设计
- 为了解决密钥的传输问题必须介绍了非对称加密技术
- 为了实现密钥的安全传输,引入了DH密钥交换协议和PKI证书体系
- 最后介绍了ECDH协议,它RSA非对称加密,安全性更高。
XOR与填充
加解密技术的核心是异或运算
- 比如明文为
1011密钥为0101进行异或运算得到 密码1110 - 拿到密码之后与密钥再进行异或运算 得到
1011即明文!
异或运算的好处是 执行速度非常快,执行一遍即可
填充
- 前面执行异或运算的前提是 明文和密钥长度是一样的,但通常密钥不可能那么长
- 那么就需要对明文分成多组,每组与密钥长度一致, 当最后一个明文块长度不够时需要填充
分组工作模式
我们来讨论下实现加密技术如何对明文进行分组。
ECB模式
最简单的分组模式时ECB模式,直接将明文分解为多个块,对每个块独立加密
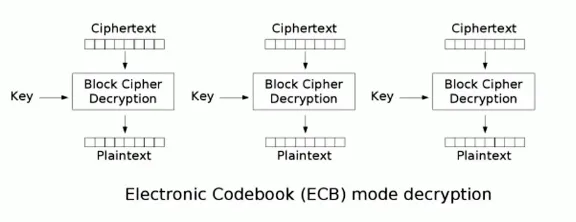
这种模式的缺点是无法隐藏数据特征

我们实际期望的是全躁点

CBC模式
我们改进一下方案, 每个明文块先与前一个密文块进行异或后,再进行加密,这样就消除了躁点
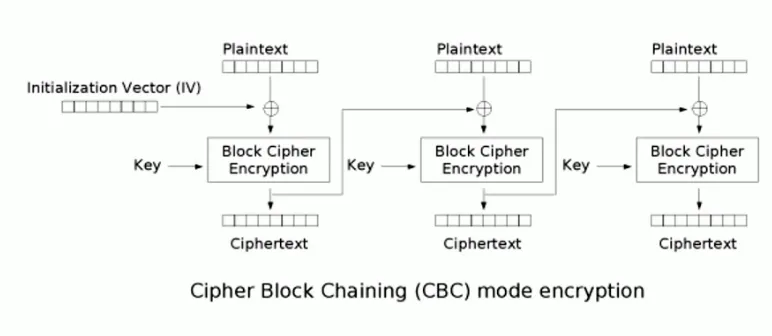
这种方式的缺点是: 加密过程串行化, 无法利用多核CPU的优势
CTR模式
如果 通过递增一个加密计数器以产生连续的密钥流 进行加密如何呢? 可以对内容进行分片,从而利用多核CPU进行加密
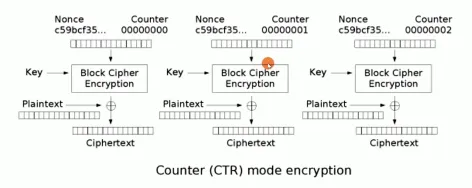
这种方式的确解决了利用多核CPU优势的问题,仔细分析还有个问题是,无法验证消息的完整性(网络上数据传输可能丢失,而我们不知道)
hash函数验证消息的完整性
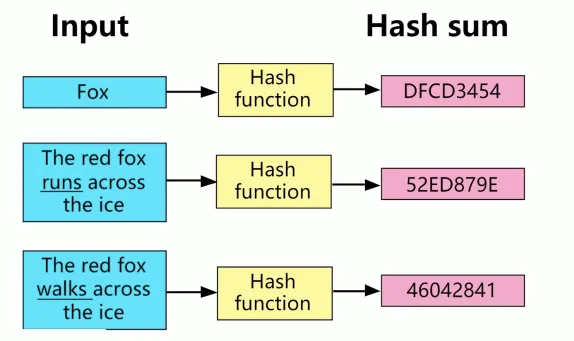
- hash函数的特征, 无论输入多长的内容, 经过hash函数后,可以得到一个定长的较短的hash编码
- hash编码可以理解为子文
- 通常一个好的hash函数,会使得不同的输入很难得到相同的值(也就是碰撞概率很低)
MAC(Message Authentication Code)算法是 hash函数的一种
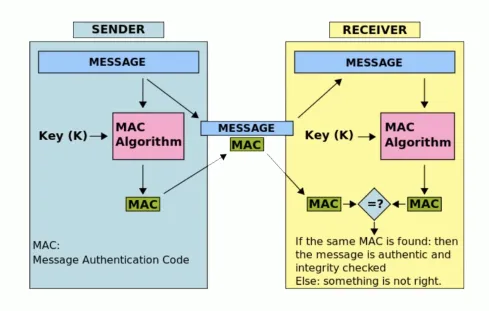
- 我们将消息(MESSAGE)经过MAC算法处理 得到 摘要1(MAC)
- 我们再将摘要和密文一起发送给接收者
- 接收者接受的密文, 使用密钥解密出原文, 再将原文进行MAC算法处理 得到的摘要2和原来的摘要1进行对比,就可以验证消息是否完整
有了MAC函数就有了GCM
GCM工作模式
GCM = CTR + GMAC
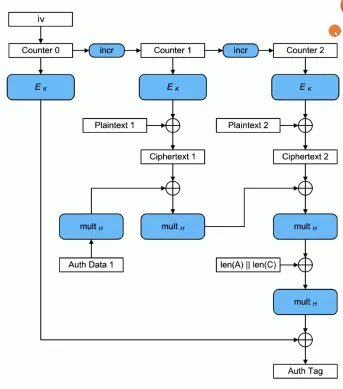
对于密文进行MAC算法得到hash
AES对称加密算法
AES(Advanced Encryption Standard)
-
为比利时密码学家Joan Daemen和Vincent Rijmen所设计,又称Rijindael加密算法
-
常用填充算法: PKCS7
-
常用分组工作模式: GCM
-
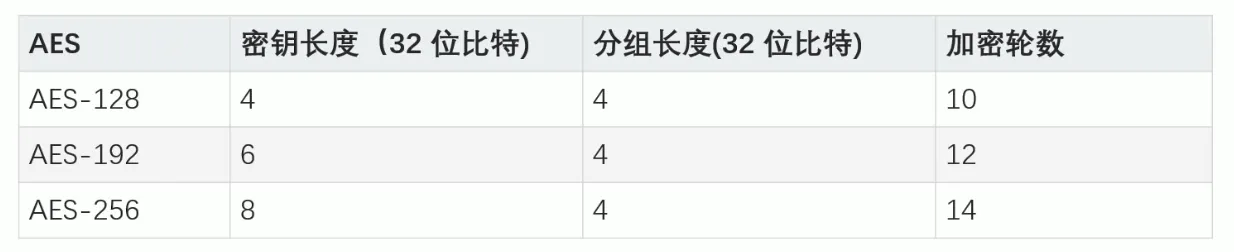
AES的三种密钥长度
-
AES分组长度是128位(16字节)
AES加密步骤
- 把明文按照128bit (16字节)拆分成若干个明文块,每个明文块是4*4矩阵
- 按照选择的填充方式来填充最后一个明文块
- 每一个明文块利用AES加密器和密钥,加密成密文块
- 拼接所有的密文块,成为最终的密文结果
不管AES如何安全,那么它如何将密钥传送给对方呢?非对称加密就可以解决这个问题。
非对称加密
- 每个参与方都有一对密钥 即 公钥和私钥
- 公钥向对方公开, 私钥仅自己使用
- 你给对方发消息 使用自己的私钥加密,另外还要将自己的公钥发给对方, 对方得到密文使用你的公钥解密
- 对方给你发消息 使用你的公钥加密, 你收到密文后使用自己的私钥解密
常用的非对称加密算法: RSA
非对称加密的应用: PKI证书体系、DH密钥交换协议
RSA非对称加密算法
1. 我们先看一下公钥和私钥如何产生

我们选取了p=11 q=29 k=3,按照上述流程得到
- 公钥(3,319)
- 私钥(187,319)
2. 有了公钥和私钥,我们再看一下加解密过程

按照上述流程我们来验证一下
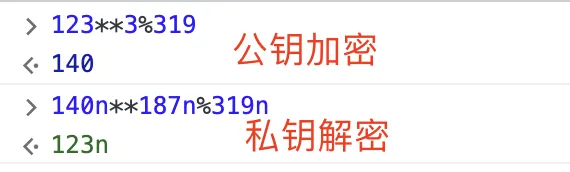
我们在选一个数 26吧,进行私钥加密公钥解密
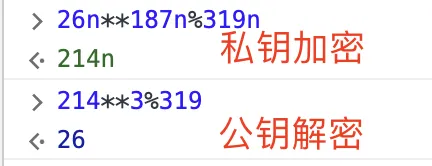
因为涉及大量乘法,所以非对称加密很耗费性能
注意: 明文 要小于 p和q的乘积n, 如我们 选取明文320(320>319) 加密后就无法进行解密
思考:为什么公私钥加密是安全的呢?
参考第一张图
- 假设我们拿到了 公钥(k,n) 能不能推导出私钥(d,n)呢
- n已经有了,只要找到d
- 由于k是随机选的,只要找到v,就能找到d
- v=(p-1)(q-1),由于n是一个很大的数字,对n进行质数因式分解是很困难的
- 所以AES算法的安全性在于对一个大数字进行因式分解是很困难的
使用openssl生成公私钥证书
- 生成私钥(公私钥格式参见RFC3447)
openssl genrsa -out private.pem - 从私钥中提取出公钥
openssl rsa -in private.pem -pubout -out public.pem - 查看ASN.1格式的私钥
openssl asn1parse -l -in private.pem

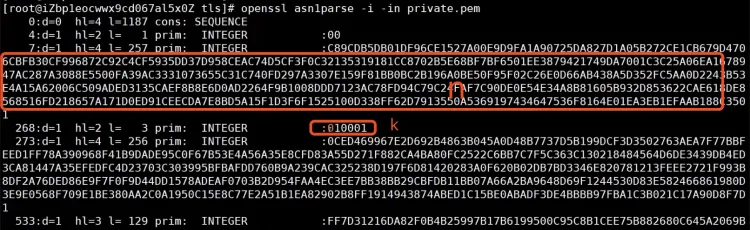
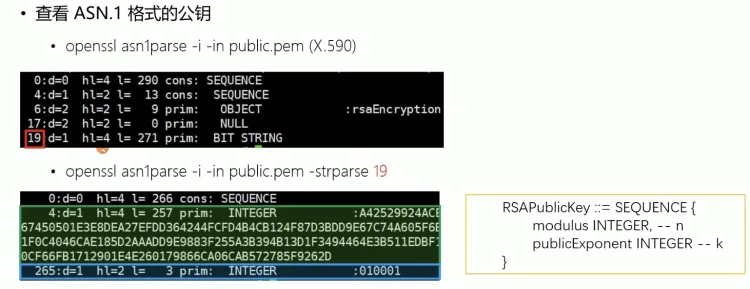
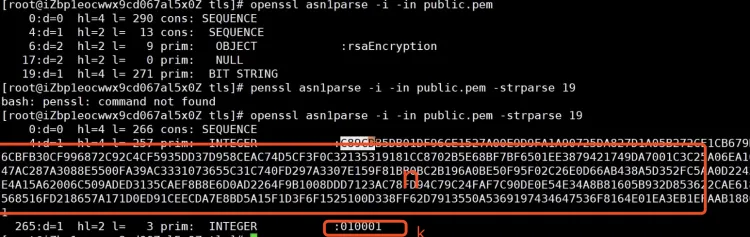
PKI证书体系
PKI证书体系是非对称加密的应用
为什么需要PKI证书体系
- Web世界是开放互联的,很多时候我们是第一次访问该网站, 如何获取网站的公钥呢?
- 通过通过握手的方式, DNS被劫持,服务端发送的消息就被破解了
- 与现实生活中问题买房子,证明这个房子是我的,需要房产证一样,网络中的这些机构组成了PKI证书体系
公钥的管理: Public Key Infrastructure (PKI) 公钥基础设施
- 由Certificate Authority (CA) 数字证书认证机构将用户个人身份与公开密钥关联在一起
- 公钥数字证书组成
CA信息、公钥用户信息、公钥、权威机构的签字、有效期 - PKI用户
- 向CA注册公钥的用户
- 希望使用已注册公钥的用户
签发证书流程
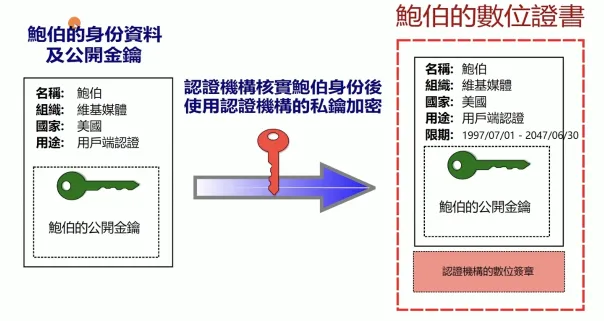
签名与验签流程
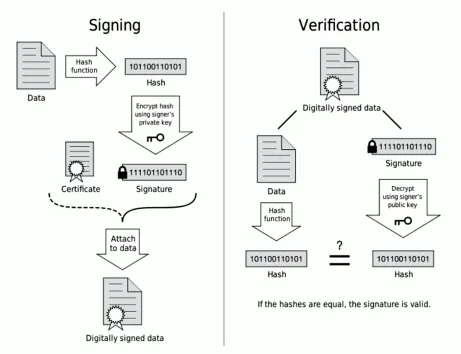
证书信任链
证书分类
- DV证书
- OV证书
- EV证书
DH 密钥交换协议
在TLS/SSL握手中,DH协议是一种常用的算法,用来沟通协商出后面对称加密所使用的密钥
DH协议的背景(RSA密钥交换的问题)
事实上 我们使用RSA算法所生成的公私钥,基于这些公私钥生成对称加密所使用的密钥也是可行的
具体流程如下:
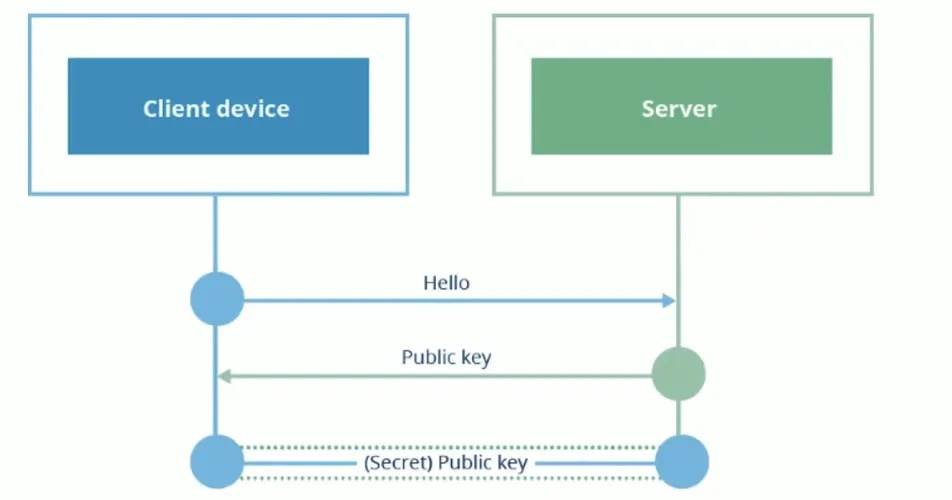
- 客户端发送 hello 到服务端
- 服务端将公钥发给客户端
- 客户端生成一个密码(只有它自己知道)使用前一步的公钥加密 发给服务端
- 服务端使用私钥解码得到密码, 只有都使用这个密码进行对称加密传输数据
有人会说这个模型有个问题是服务端的消息会被机密,这个我们可以通过PKI证书体系传递公钥解决服务端消息的保密性。这里我们讨论另一个问题,消息的前向保密性
什么叫前向保密性呢? 假设有个中间人,我现在没有破解server的私钥, 我先通过网络设备,把中间的报文都保存下来,当某一天我破解了 server的私钥,我们就可计算出密码传输的密钥, 就可以对所有的消息解密了。
DH密钥交换协议,就是解决这个问题的
DH协议内容
- 它可以让双方在完全没有任何预先信息的条件下通过不安全信道创建起一个密钥
- 由于它的每一次会话密钥都是实时生成的, 所以具有前向保密性
具体流程如下图;
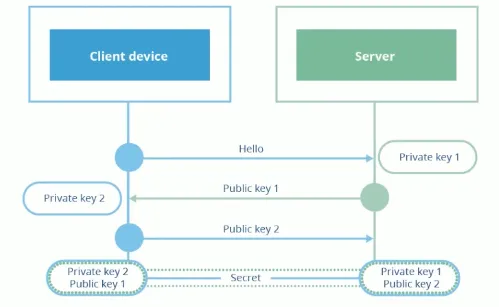
- 客户端发送 hello 到服务端
- 服务端生成公私钥(
publickey1privatekey1)把自己的公钥publickey1发给客户端 - 客户端生成公私钥(
publickey2privatekey2)并将publickey2发给服务端 - 通过一种算法,使得客户端使用
privatekey2和publickey1生成的密钥 与 服务端使用privatekey1和publickey2生成的密钥一致
这样即使 privatekey1被破解, 由于 privatekey2 不会知道, 所以还是无法破解之前保存的报文, 从而具有前向保密性
具体示例如下图
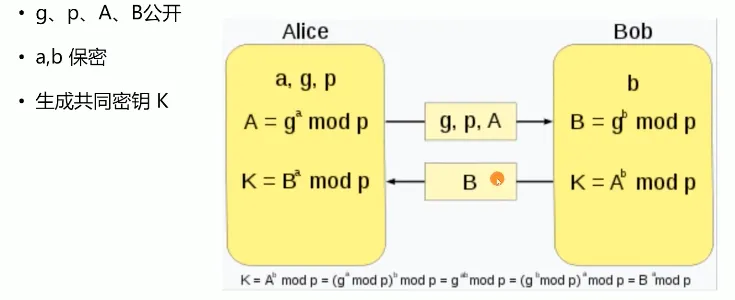
- A、a分别是Alice的公钥和私钥
- B、b分别是Bob的公钥和私钥
- K就是协商出的密钥
- g和p两个随机数是公开的,另外再把两个公钥A、B公开
我们来验证一下
jsvar p = 23n, g = 5n; // 公开数
var a = 6n, b = 15n; // 双方私钥
var A = g**a % p;
var B = g**b % p;
var K1 = A**b % p;
var K2 = B**a % p;
console.log(K1 === K2, A, B, K1, K2); // true 8n 19n 2n 2n
// p g a b可以随便调整, K1与K2值不变
DH密钥交换协议存在一个问题 中间人攻击
- 中间人拦截 A与B的通信
- 先假装自己是B,与A通信,破解A的消息
- 再假装自己是A,与B通信,破解B的消息
Q: 什么情况下会出现中间人攻击呢?
A: 代理工具、DNS劫持等。
解决方案就是引入第三方 解决身份验证问题, 即KPI证书体系
ECDH协议
由于DH密钥交换协议有两个问题
- 涉及大量乘法运算,所以很耗性能
- 它的安全基于大因数分解比较困难,所以通常需要很长的位数
现在互联网中主要使用的是ECDH密钥交换协议,它其实是DH密钥交换的升级,它基于ECC椭圆曲线的特性来实现
ECC椭圆曲线的特性
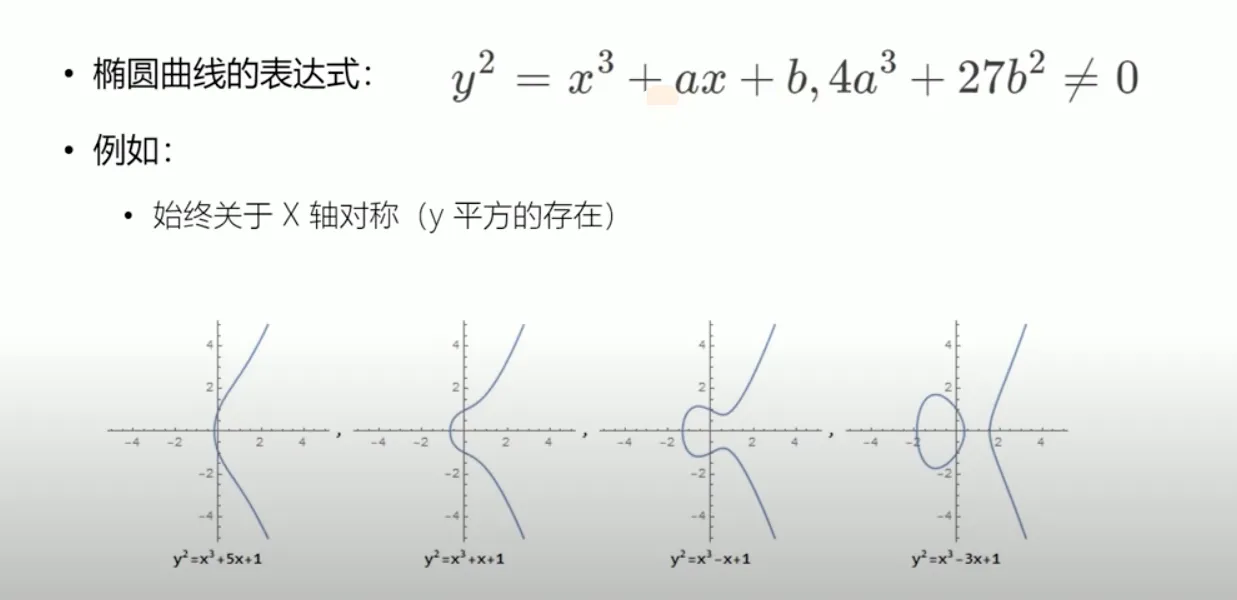
上图 就是维尔斯特拉斯椭圆函数
椭圆曲线始终沿X轴对称。
从上面四张图来看,它跟椭圆无关,之所以叫做椭圆曲线,是因为它在计算某些属性的时候与计算椭圆弧长相关的属性具有相似之处。
ECC曲线的特性: +运算
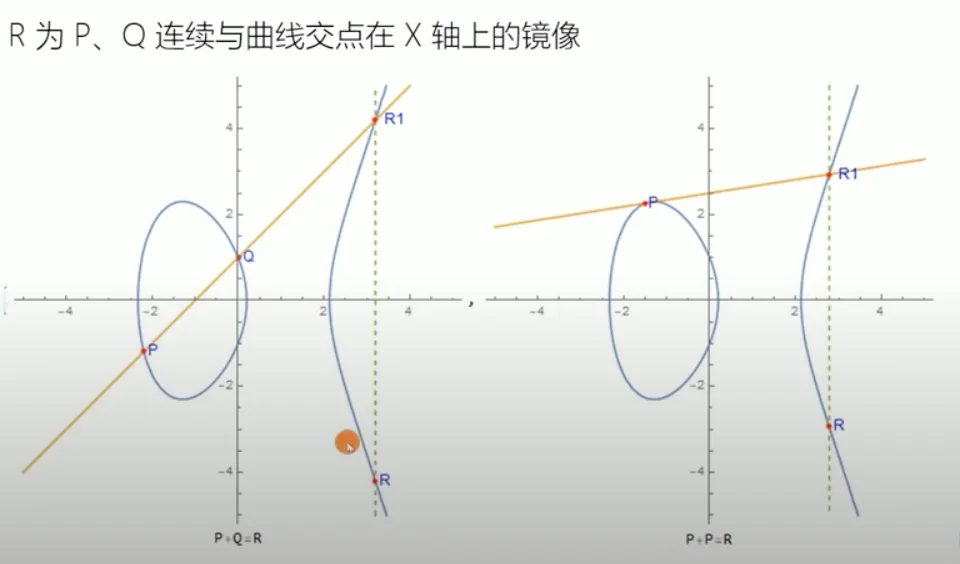
这里的+运算并非数学中的+运算,只是一种假设运算,利用数学中+运算的特性(结合律、交换律)
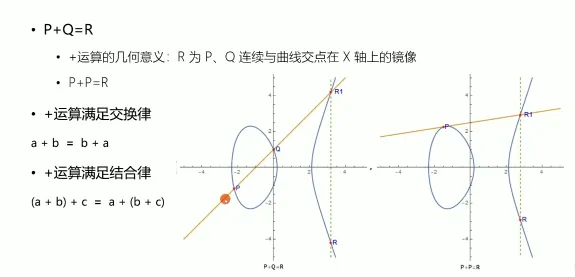
P和Q是曲线上的两点,P和Q连线交与曲线R1点,R是R1关于X轴的对称点,也在曲线上.
假设 ,那么 ,即
如果 P和Q是同一点,则
例子
- 设曲线
- , 在曲线上 求 点坐标
- P在曲线上
- Q在曲线上
我在这个网站绘制了一张图
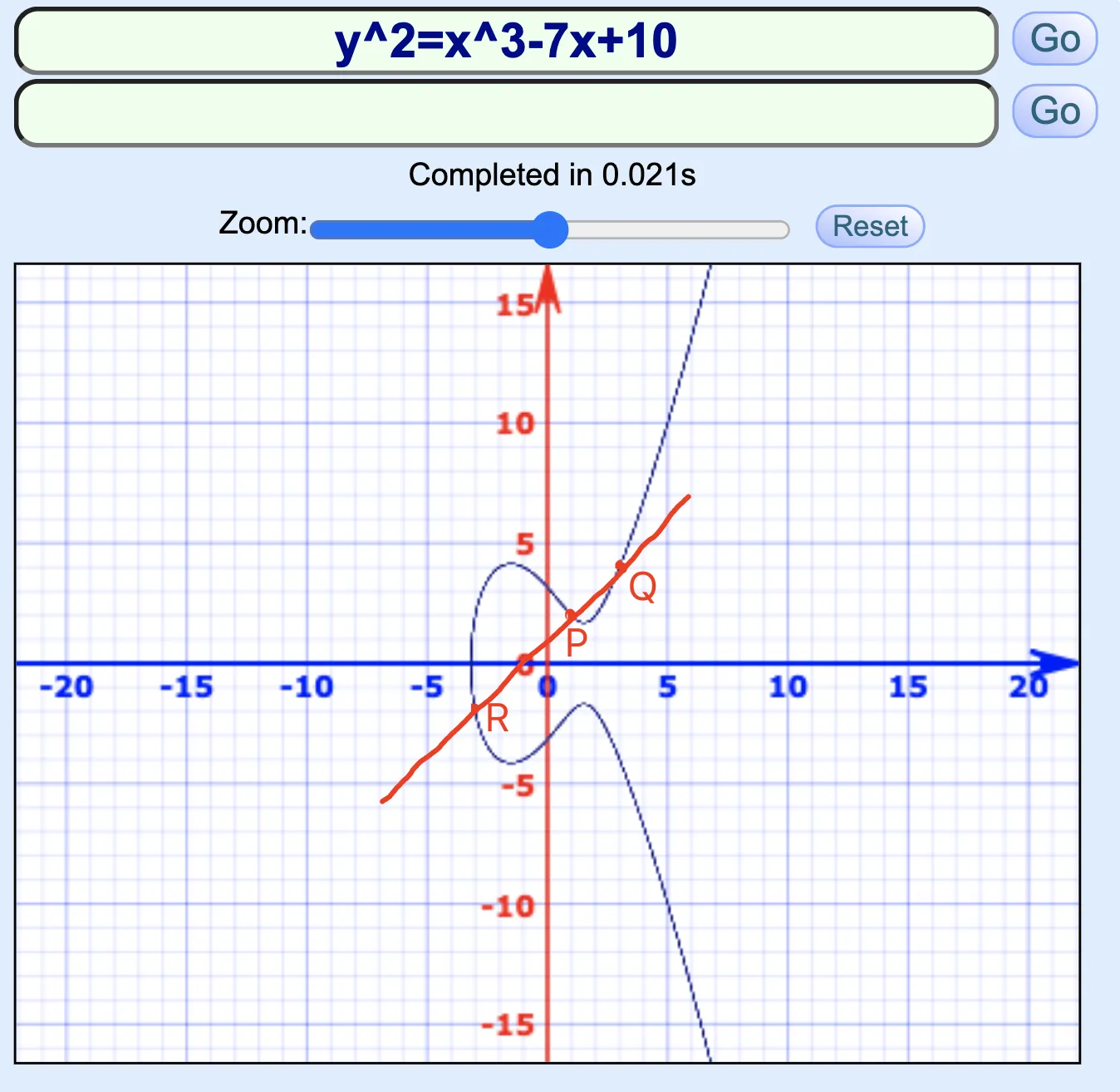
求解 有个公式
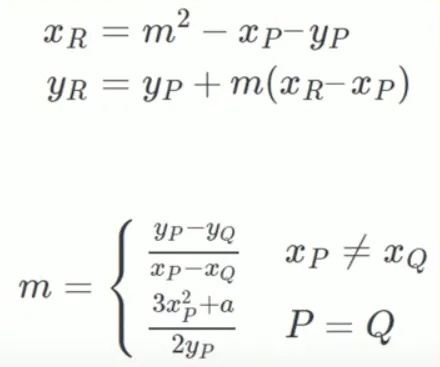
- 是斜率
- 是R点X轴坐标
- 是R点Y轴坐标
以上就是椭圆曲线+运算的几何意义和代数意义。那么它与加解密有什么关系呢?
ECC的关键原理
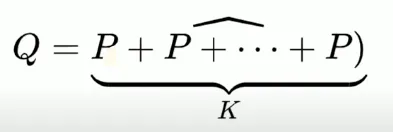
- 已知K与P,求解Q容易,即加密过程正向运算快,
- 已知Q与P,计算K困难,即破解密钥逆向运算非常困难
为什么正向运算快? 这里有个可以借助指数运算
- 对点做切线 按前面的公式求出
- 对点做切线 按前面的公式求出
逆向运算,已知Q与P,求出多少个K,这是没有规律的,只能暴力求解。
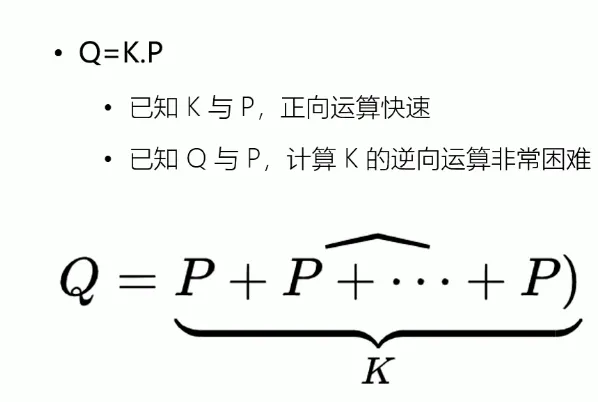
这个公式里 是已值的, 是公钥, 就是私钥。
ECDH协议
ECDH协议就是DH协议使用椭圆曲线ECC后的变种,优点是比DH计算速度快,同等安全条件下密钥更短

非对称加密总结
前面讲了非称加密有两种方案
- 第一种是基于大因数分解困难的RSA非对称加密算法
- 对于中间人攻击、DNS劫持等引起的服务端消息的保密性引入PKI证书体系
- 公钥是用来暴露给别人,让别人给你发消息用的,私钥用来解密接受的消息,你回复消息需要私钥加密,别人通过你的公钥解密。
- 为了解决消息的前向保密性引入DH密钥协议,具体算法为
- 已知 g和p 两个公开数,双方各自生成私钥a和b
- 使用公式
g**私钥 % p生成各自的公钥A和B进行交换 - 通过
对方公钥**自己私钥 % p, 双方得到同一个密钥K - 通过这个密钥K,双方就可以使用对城加密传输数据了。
- 第二种是ECDH协议,更加安全。借助椭圆曲线公式上和定义一种
+运算实现求解困难验证容易。
本文作者:郭敬文
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!