目录
学习 es6数值的扩展 有几点疑惑
0.1 + 0.2与0.3为什么不相等?- 为什么
3.0000000000000002 === 3表达式为true?- 为什么超过精度的数值可正确显示,但由其计算得出的结果可能不准确?
0+0-0是什么关系 ?- ES6
Map+0-0是同一个key,Object.is(+0, -0)为false,+0 === 0为true- “JavaScript 采用 IEEE 754 标准,数值存储为64位双精度格式,数值精度最多可以达到 53 个二进制位(1 个隐藏位与 52 个有效位)” 这句话想不明白,为什64位双精度就变成52个有效位,一个隐藏位是什么 小数点还是符号?
- 二进制运算
^<<<>>- N年前学习的计算机原理 源码、反码、补码 答案肯定在这里,但此刻已经记忆比较模糊了
计算机运算
二进制
背景
首先要说一个问题,计算机为什么要采用二进制,而不是十进制?
- 其实早期电子元件也尝试过10进制3进制等,但性能不好容易出错;
- 后来采用了二进制主要是技术实现简单,计算机是由逻辑电路组成,逻辑电路通常只有两个状态,开关的接通与断开,这两种状态正好可以用“1”和“0”表示。
知乎 :为什么计算机一定要用二进制?
计算机本身的理论模型,和采用哪个数学上的进制完全无关,十进制也好,五进制也好,二进制也好,进制在数学上都是等价的,并没有哪个进制拥有其他进制无法实现的计算。 但计算机的实现是个工程问题,需要和真实的物理环境打交道,我们现在是用电路去实现我们的计算机模型,那就需要和物理电路打交道,需要考虑到信号的衰减延迟,电路器件的各种电气特性,什么电磁波干扰电流扰动,也就是会有失真的情况出现,而要最大程度避免衰减,失真对计算机这个完美世界造成破坏,同时要考虑电路的设计,制作成本,就需要最简单化的物理实现方案。 电子计算机确实是可以做成十进制的,就像题主说的像灯泡亮度分成十种亮度那样,但与此同时会出现很多的工程问题,比如对电子器件的精度和稳定性要求很高,电路设计的复杂性提升等等,到头来还不如就用二进制,在成本和质量上最划算。 现实是很残酷的,就算采用了二进制这种最简单最不容易出错的方案,计算机运行都还有很多出错的时候,我们的内存条也要ECC之类的纠正机制,这还是在地球大气层保护之下,上了太空就更恶劣了。
概念
参考资料: 一文读懂原码、反码与补码
为运算方便,机器数有 3 种表示法,即原码、反码和补码。
原码
原码是一种计算机中对数字的二进制定点表示法。原码表示法在数值前面增加了一位符号位
反码
- 正数的反码和原码一样,
- 负数的反码就是在原码的基础上符号位保持不变,其他位取反。
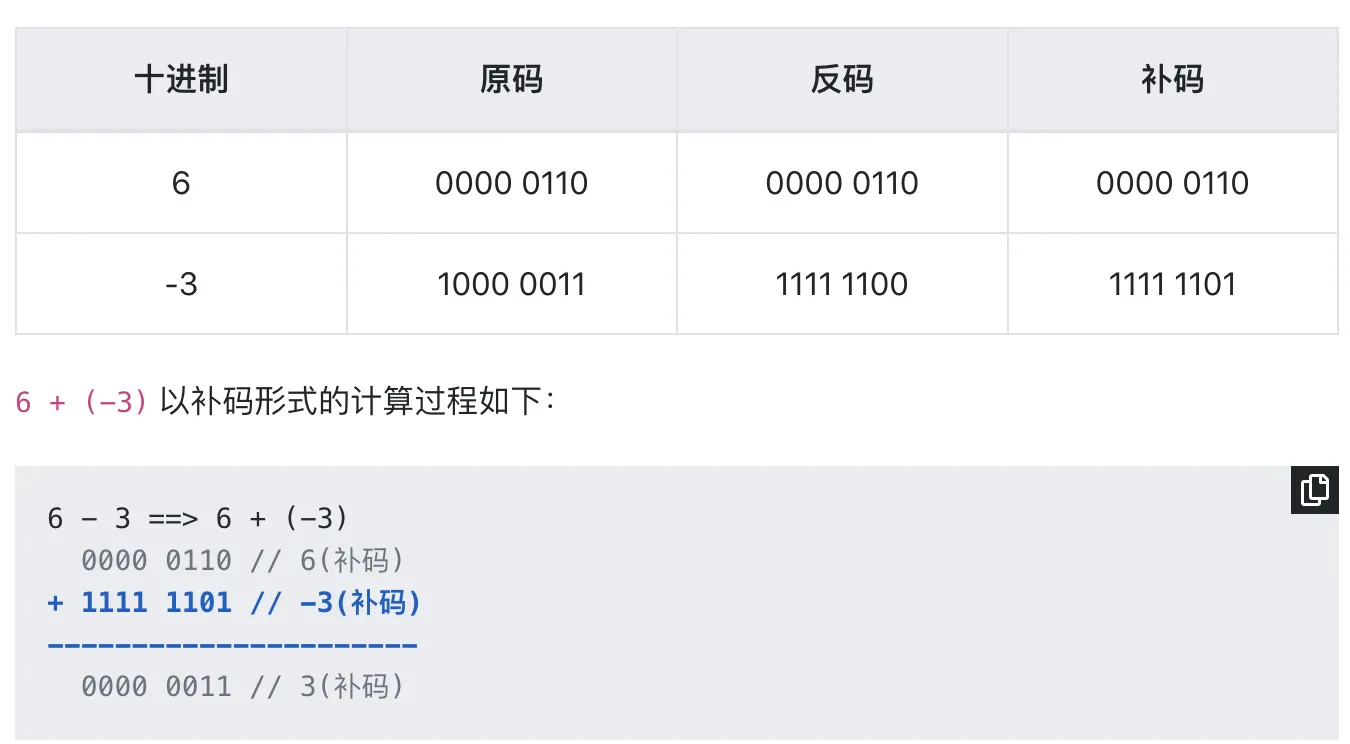
补码
- 正数和 0 的补码就是该数字本身。
- 负数的补码则是将其对应正数按位取反再加 1
加减运算
正数与负数 ,加法与减法交叉运算,共八种组合,(0这里理解为正数)
| a | 运算 | b | |
|---|---|---|---|
| 正数 | + | 正数 | a+b |
| 正数 | - | 正数 | a-b |
| 负数 | + | 负数 | -a-b ---> -(a+b) |
| 负数 | - | 负数 | -a+b ---> -(a-b) |
| 正数 | + | 负数 | a-b |
| 正数 | - | 负数 | a+b |
| 负数 | + | 正数 | -a+b ---> -(a-b) |
| 负数 | - | 正数 | -a-b ---> -(a+b) |
总结:
两个数运算可简化为:两个正数a与b先加减运算再符号运算
- 先忽略符号位 要么 a+b 要么 a-b,假设结果为c
- 符号由a的符号决定
- 最终的结果为c的符号位与a的符号位运算得到的值
a+b运算, 正数+正数 逢2进1,
a-b 以 6+(-3)举例
小结
回顾一下文章开头的7个问题
问题7 原码反码补码是什么?
- 原码表示法在数值前面增加了一位符号位;
- 反码 正数的反码和原码一样,负数的反码就是在原码的基础上符号位保持不变,其他位取反。
- 补码 正数和 0 的补码就是该数字本身。负数的补码则是将其对应正数按位取反再加 1
- 反码补码概念的提出是为了 方便计算机运算(不用考虑符号位或者让符号位直接运算)
问题4 +0 0 -0是什么关系?为什么会有三个概念?
+0和0是同一个数,无任何区别- **因符号位的存在所以
0有两种表示方式+0和-0 - 正因为如此所以8位固定长度能表示的范围为【-127, 127】 共28-1即255个数**
问题5 JS中+0 与 -0的区别
- es5
+0 === -0为true - es6
Map中+0和-0是同一个key;Object.is(+0, -0)返回false Object.ises5实现if (x === y) { return x !== 0 || 1 / x === 1 / y; }
位移运算
左移(<<)
该操作符会将第一个操作数向左移动指定的位数。向左被移出的位被丢弃,右侧用 0 补充。

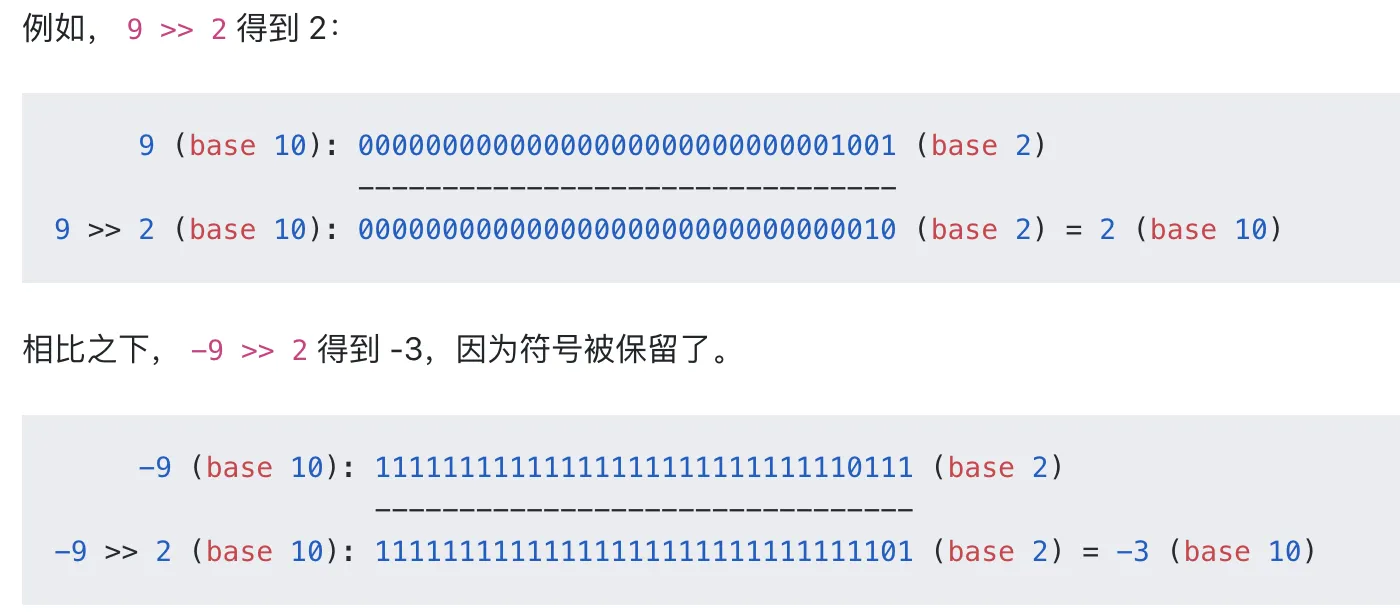
有符号右移(>>)
该操作符会将第一个操作数向右移动指定的位数。向右被移出的位被丢弃,拷贝最左侧的位以填充左侧。由于新的最左侧的位总是和以前相同,符号位没有被改变。所以被称作 “符号传播”。
无符号右移(>>>)
该操作符会将第一个操作数向右移动指定的位数。向右被移出的位被丢弃,左侧用 0 填充。因为符号位变成了 0,所以结果总是非负的。
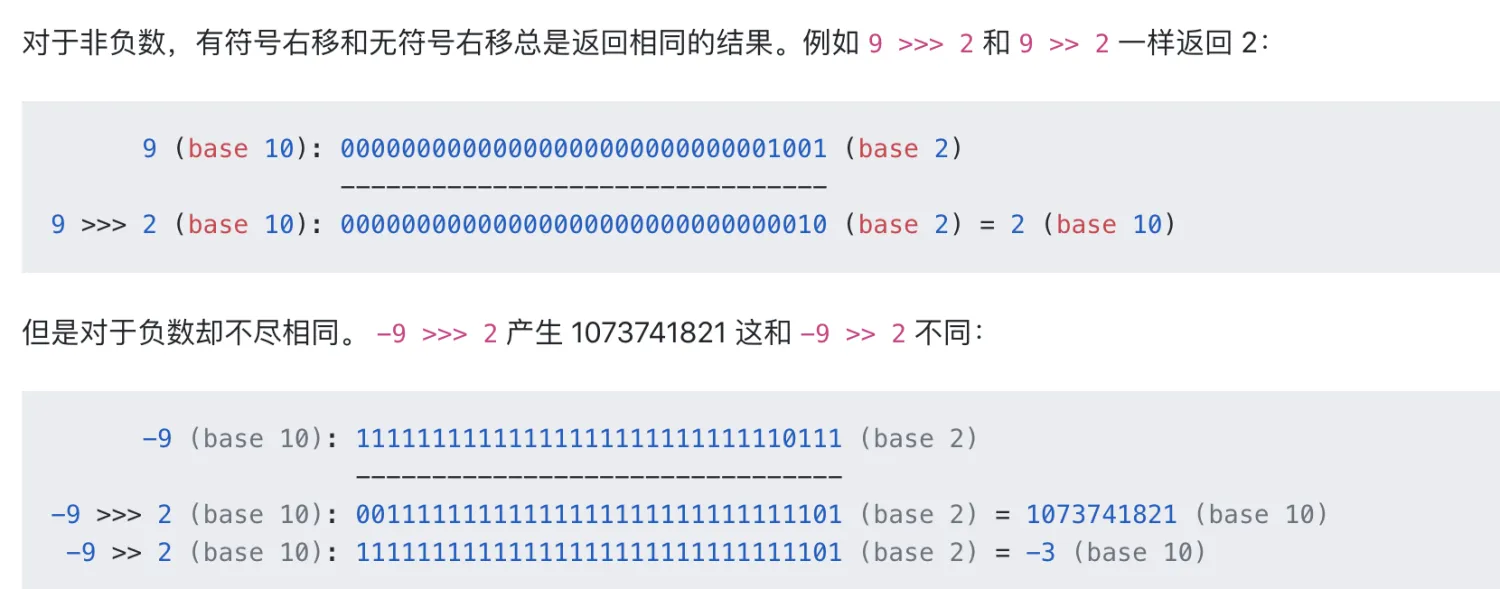
~ 按位求反 JS实现:改变符号并减1



进制之间转换
整数部分转换
- 二进制转十进制
00 100 010
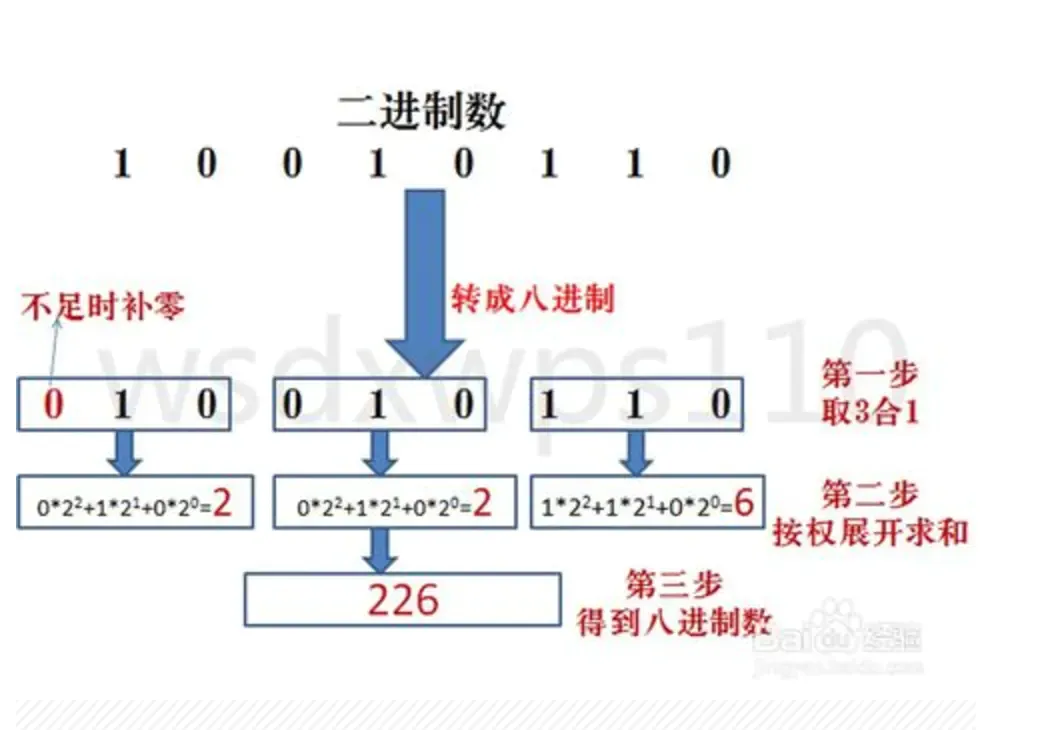
- 二进制转八进制
二进制
10 010 110
八进制226
-
二进制转十六进制与二进制转八进制类似,
-
八进制转二进制,每1位八进制数用3位二进制数表示,(二进制转八进制的逆操作)
八进制数
6对应二进制110
6 与 比较 前者不小于后者 则百位数字为1
6- = 2
2 与 比较 前者不小于后者 则十位数字为1
2- 2 = 0
0 与 比较 前者小于后者 则个位数字为0
-
八进制转十进制 (不难看出,与二进制转十进制类似)
-
八进制转十六进制 与 二进制转八进制类似, 每两位2进制数字合成一位十六进制数字
-
十六进制转二进制,与八进制转二进制类似
-
十六进制转八进制,与八进制转二进制类似
-
十六进制转十进制,同二进制转十进制, 如 十六进制数
0x0a77 * (16**0) + 10 * (16**1) = 167 -
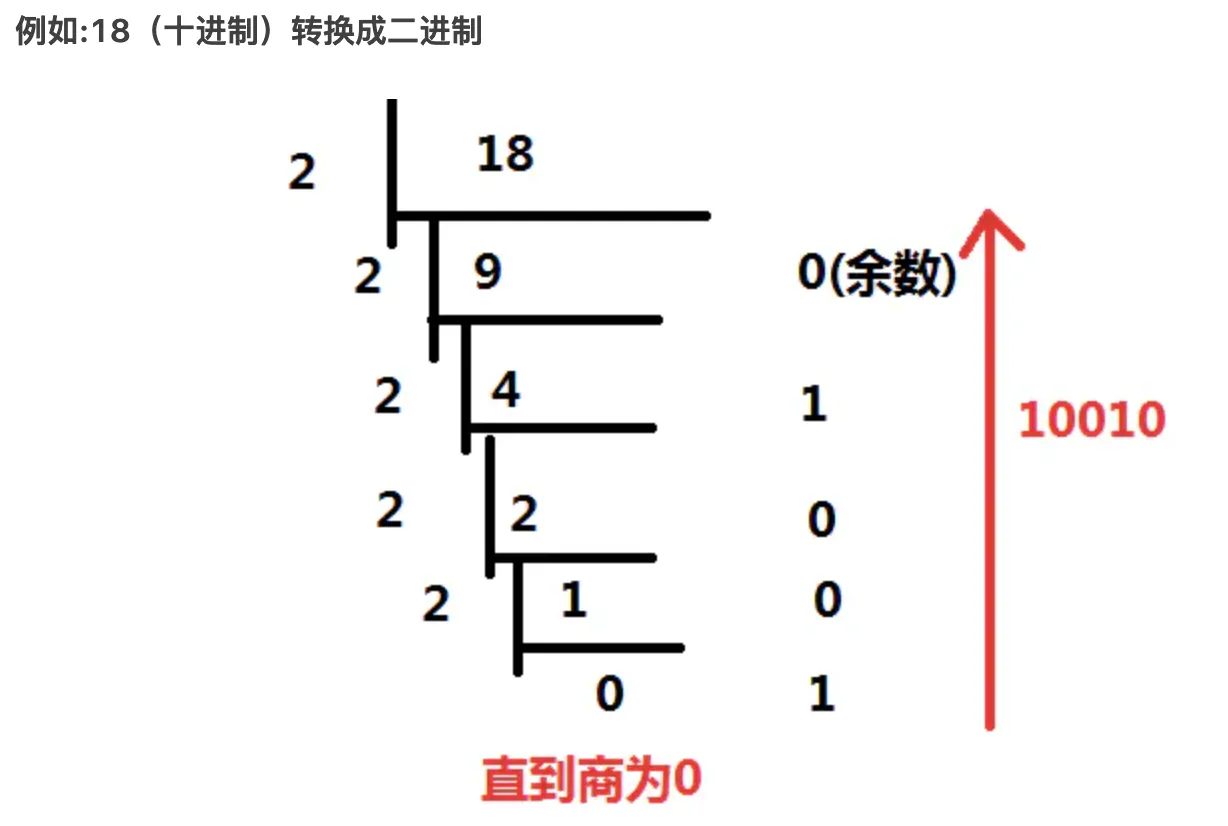
十进制转二进制
- 十进制转八进制 与十进制转二进制类似
- 十进制转十六进制 与十进制转二进制类似
总结:只需记住 二进制转十进制 十进制转二进制 二进制转八进制 八进制转二进制 四种转换即可
小数部分转换
二进制转十进制
举个例子: 以二进制小数1100.0011为例

为计算方便
后序示例数字直接忽视整数部分,
只探讨 二进制转十进制 十进制转二进制 二进制转八进制 **八进制转二进制 **四种转换
十进制转二进制
以 十进制小数
0.625为例
0.625 * 2 = 1.250 取整数部分1
0.25 * 2 = 0.5 取整数部分 0
0.5 * 2 = 1 取正数部分1 , 由于没有小数部分了计算终止,得到 二进制数0.101
代入 二进制转十进制运算 1*(2**(-1)) + 1*(2**(-3)) = 0.625再举一例: 0.33 0.33.toString(2) 0.0101_0100_0111_1010_1110_0001_0100_0111_1010_1110_0001_0100_0111_11
看不出规律推测是无限循环小数
二进制转八进制
以小数点为界从左到右3位分割一段对应一位八进制数字
0.01101₂ = 0.011_010₂ = 0.32₈
0.32₈ = 3*(8**(-1)) + 2*(8**(-2)) = 0.4062510
0.40625.toString(2) // '0.32'
二进制小数转为其他进制不存在精度问题
八进制转二进制
0.37₈ = 0.3_7₈ = 0.011_111₂
0.3_7₈ = 3*(8**(-1)) + 7*(8**(-2)) = 0.48437510
0.484375.toString(8) // '0.37'
总结
- 整数进制之间转换不存在误差问题
- 含小数位的小进制转大进制(有倍数关系)不存在误差
- 大进制转小进制(十六进制、八进制、二进制之间不存在误差)
- 十进制小数转为其他进制可能存在误差
JS数值存储
标准的 double 双精度浮点数
“JavaScript 采用 IEEE 754 标准,数值存储为64位双精度格式,数值精度最多可以达到 53 个二进制位(1 个隐藏位与 52 个有效位)”

具体规则我这里就不累数,参考资料: 浅聊 JavaScript 浮点数 有兴趣可以详细了解下 以上知识点解释了问题6
下面来看一下问题2: 为什么 3.0000000000000002 === 3表达式为true
为什么 3.0000000000000002 === 3表达式为true?
手动将 3.0000_0000_0000_0002转换成二进制浮点数
整数部分为 11₂
小数部分0.0000_0000_0000_0002
0.0000_0000_0000_0002.toString(2)
'0.0000000000000000000000000000000000000000000000000000111001101001010110010100101111101100010001001101111' 注意小数点后面正好有52个0
0.0000_0000_0000_0002.toString(2).length 105
将 3.0000000000000002 用 IEEE754 格式表示
- 符号S: 正数,0
- 指数位E:11 = 1.1 * 2^1 (二进制),E = 1023 + 1 = 1024 = 10000000000(二进制)
- 尾数位M:0.1.....0 所以该浮点数格式为: 0 1000_0000_000 1...000(一共52个0) 这个数正好是
3
所以问题2 已经得到答案了
因为
采用双精度浮点数存储 能够存储的二进制数位数有限,
而十进制小数转为二进制可能是无限循环小数或者大于 double浮点数的存储空间,
丢弃多余的数字,最终导致误差产生
再看一下问题1
为什么0.1 + 0.2不等于0.3 ?
0.1.toString(2)
'0.0001100110011001100110011001100110011001100110011001101' // 57
按 IEEE754 格式 57 - 4 = 52可以精确存储
0.2.toString(2)
'0.001100110011001100110011001100110011001100110011001101' // 56
按 IEEE754 格式 56 - 3 = 53 会丢弃最后一位数
0.3.toString(2)
'0.010011001100110011001100110011001100110011001100110011' // 56
按 IEEE754 格式 56 - 2 = 54 会丢弃最后两位数
总结:
存储0.1没有误差, 存储 0.2丢弃最后一位 1 存储0.3丢弃最后2位 11,
显然存储0.3丢弃的数值>存储0.2丢弃的数值
经分析 0.1 + 0.2 应该大于 0.3
0.1 + 0.2 > 0.3//true
为什么超过精度的数值可正确显示,但由其计算得出的结果可能不准确
对于整数,最多能精确显示16个十进制位,超过会被截断。 对于小数,最多能精确显示小数点后16个十进制位,超过会被截断。
首先看一下浮点数的特点
- 64位浮点数与64为整形数相比存储数的总量不变
2 ** 64 - 但是浮点数表示的范围更大,整数尾部0可以省略(指数位加1), 小数位小数点后面的连续0可以省略(指数位加-1)
- 为什么划分安全整数? (
Number.MIN_SAFE_INTEGER,Number.MAX_SAFE_INTEGER)- 对于一个数53位, 低位可能会丢失,位数越多,运算越会不准确
- 因浮点数的特点,整数尾部的连续0可提取的指数位,所以超过安全数区间的数值可与你正常显示,又因运算是可能存在低位丢失所以运算结果可能不准确
- 误差校验依据
Number.EPSILION2 ** -52最小浮点数1与整数1 之差- 一般认为 当两数相减是 绝对值小于这个数 就可能存在误差,
- 值越小说明存在误差的可能性更大,比这个值大也可能存在误差
Number.MIN_VALUENumber.MAX_VALUE- 浮点数能表示的最小值、最大值,
- Number.MIN_VALUE.toString(2).length
- 指数位排除符号能调试的位数2**10,+ 52个有效数位 = 1076
大整数相乘
javascript/**
* 大整数相乘 思路
* 1. 检查输入的合法性(非空, 无非法字符串)
* 2. 检查输入是否可以简单运算(一个数为0、-1、1、+1)
* 3. 去掉最前面可能有的正负符号,并判断输出的正负
* 4. 将输入的值分四段一截,(分的太短性能太差,分的太长可能造成精度丢失)
* 5. 遍历相乘得到最终数组(递归)
* 6. 遍历最终数组,拼接最终的数
* 7. 将正负符号与最终的数拼接输出
*/
function bigNumberAdd(str1, str2) {
// 1. 检查输入的合法性(非空, 无非法字符串)
if(typeof str1 !== "string" || Number.isNaN(+str1)) {
throw new Error('params 1 must String and can transform to Number')
}
if(typeof str2 !== "string" || Number.isNaN(+str2)) {
throw new Error('params 2 must String and can transform to Number')
}
// console.log(BigInt(str1) * BigInt(str2));
// 2. 检查输入是否可以简单运算(一个数为0、-1、1、+1)
if(['0', '-1', '+1', '1'].includes(str1)) {
if(str1 === '0') return 0;
if(str1 === '-1'){
str2 = str2.replace(/^-/, '')
};
str2 = str2.replace(/^\+/, '');
return str2;
}
if(['0', '-1', '+1', '1'].includes(str2)) {
if(str2 === '0') return 0;
if(str2 === '-1'){
str1 = str1.replace(/^-/, '')
}
str1 = str1.replace(/^\+/, '');
return str1;
}
// console.log(sign || '+', str1, str2)
// 3. 判断输出的正负
const sign = getSymbol();
function getSymbol() {
const sign1 = /^[-+]/.test(str1);
const sign2 = /^[-+]/.test(str2);
let symbol = ''
let symbol1 = '';
let symbol2 = '';
if(sign1) {
symbol1 = str1.substr(0, 1);
str1 = str1.substr(1);
if(symbol1 === '+') symbol1 = '';
}
if(sign2) {
symbol2 = str2.substr(0, 1);
str2 = str2.substr(1)
if(symbol2 === '+') symbol2 = '';
}
if(symbol1 !== symbol2) {
symbol = '-'
}
return symbol;
}
// 4. 将输入的值分四段一截
const arr1 = getArr(str1);
const arr2 = getArr(str2);
function getArr(str) {
return new Array(Math.ceil(str.length / 4)).fill('').reduce(
(sum, item, index) => {
const end = str.length - 4 * index;
sum.push(str.substring(Math.max(end - 4, 0), end));
return sum;
}, [])
};
console.log(sign, arr1, arr2);
// 5. 遍历相乘得到最终数组
const finallyArr = [];
for (let i=0; i<arr1.length; i++) {
for (let j=0; j<arr2.length; j++) {
updateFinallyArr(i+j, arr1[i]*arr2[j]);
}
}
function updateFinallyArr(index, num) {
const old = finallyArr[index];
if(old) {
num +=old
}
finallyArr[index] = num%10000;
if(num > 9999){
updateFinallyArr(index + 1, Math.floor(num/10000));
}
}
console.log(finallyArr);
// 6. 遍历最终数组,拼接最终的数
let finallyStr = finallyArr.map(item => (item + '').padStart(4, '0')).reverse().join('');
finallyStr = finallyStr.replace(/^0+/, '');
// console.log(sign, finallyStr);
return sign + finallyStr;
}
console.log(bigNumberAdd('-99999889', '1923123131321'));
本文作者:郭敬文
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!