目录
本文参考《JavaScript数据结构与算法第三版》一书, 系统学习梳理算法思想,包含排序算法、搜索算法、分治、贪心、动态规划、回溯算法。
排序算法
测试用例 npx vitest tests_algorithm/sort.spec.ts
tsimport { describe, test, expect, beforeEach } from 'vitest';
import {
bubbleSort,
selectSort,
insertSort,
mergeSort,
quickSort,
quickSort2,
countingSort,
bucketSort,
heapSort,
radixSort,
shellSort,
} from '../ts_algorithm/sort';
describe('test 排序算法', () => {
let arr: number[];
beforeEach(() => {
arr = [6, 5, 8, 7, 2, 0, 3, 1, 4, 9];
});
test('冒泡排序', () => {
expect(bubbleSort(arr)).toEqual([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]);
});
test('选择排序', () => {
expect(selectSort(arr)).toEqual([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]);
});
test('插入排序', () => {
expect(insertSort(arr)).toEqual([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]);
});
test('归并排序', () => {
expect(mergeSort(arr)).toEqual([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]);
});
test('快速排序', () => {
expect(quickSort(arr)).toEqual([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]);
});
test('快速排序-空间复杂度优化', () => {
expect(quickSort2(arr)).toEqual([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]);
});
test('计数排序', () => {
expect(countingSort(arr)).toEqual([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]);
});
test('桶排序', () => {
expect(bucketSort(arr)).toEqual([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]);
});
test('堆排序', () => {
expect(heapSort(arr)).toEqual([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]);
});
test('基数排序', () => {
expect(radixSort(arr)).toEqual([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]);
});
test('希尔排序', () => {
expect(shellSort(arr)).toEqual([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]);
});
});
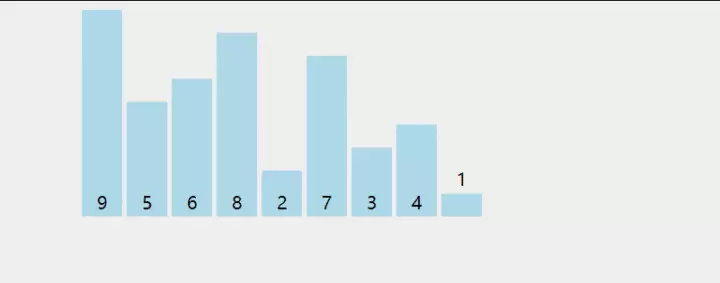
冒泡排序
比较相邻连个元素之间的大小,如果前面的比后面的大就交换位置
tsexport function bubbleSort(arr: number[]) {
for (let i = arr.length - 1; i > 0; i--) {
let flag = false;
for (let j = 0; j < i; j++) {
if (arr[j] > arr[j + 1]) {
flag = true;
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
}
}
if (!flag) {
// 剪枝优化
break;
}
}
return arr;
}
选择排序
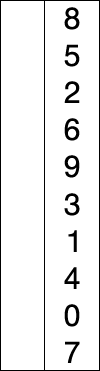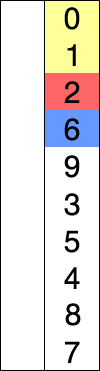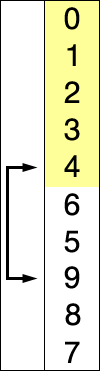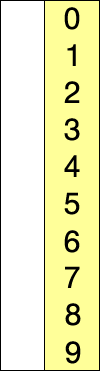
tsexport function selectSort(arr: number[]) {
for (let i = 0; i < arr.length - 1; i++) {
let minIndex = i;
for (let j = i; j < arr.length; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
if (minIndex !== i) {
[arr[minIndex], arr[i]] = [arr[i], arr[minIndex]];
}
}
return arr;
}
插入排序
我们在玩打牌的时候,你是怎么整理那些牌的呢?一种简单的方法就是一张一张的来,将每一张牌插入到其他已经有序的牌中的适当位置。当我们给无序数组做排序的时候,为了要插入元素,我们需要腾出空间,将其余所有元素在插入之前都向右移动一位,这种算法我们称之为插入排序。
- 左边是有序区,右边是无序去
- 依次拿无序去的每一个元素与有序区进行比较(从右往左比较),找到一个合适的位置(左边的元素比他小右边的元素比他大),插进去
tsexport function insertSort(arr: number[]) {
for (let i = 1; i < arr.length; i++) {
const it = arr[i];
// 这里可以二分查找优化
for (let j = 0; j < i; j++) {
if (it < arr[j]) {
[arr[i], arr[j]] = [arr[j], arr[i]];
}
}
}
return arr;
}
归并排序
将一个大的无序数组有序,我们可以把大的数组分成两个,然后对这两个数组分别进行排序,之后在把这两个数组合并成一个有序的数组。由于两个小的数组都是有序的,所以在合并的时候是很快的。
通过递归的方式将大的数组一直分割,直到数组的大小为 1,此时只有一个元素,那么该数组就是有序的了,之后再把两个数组大小为1的合并成一个大小为2的,再把两个大小为2的合并成4的 ..... 直到全部小的数组合并起来。
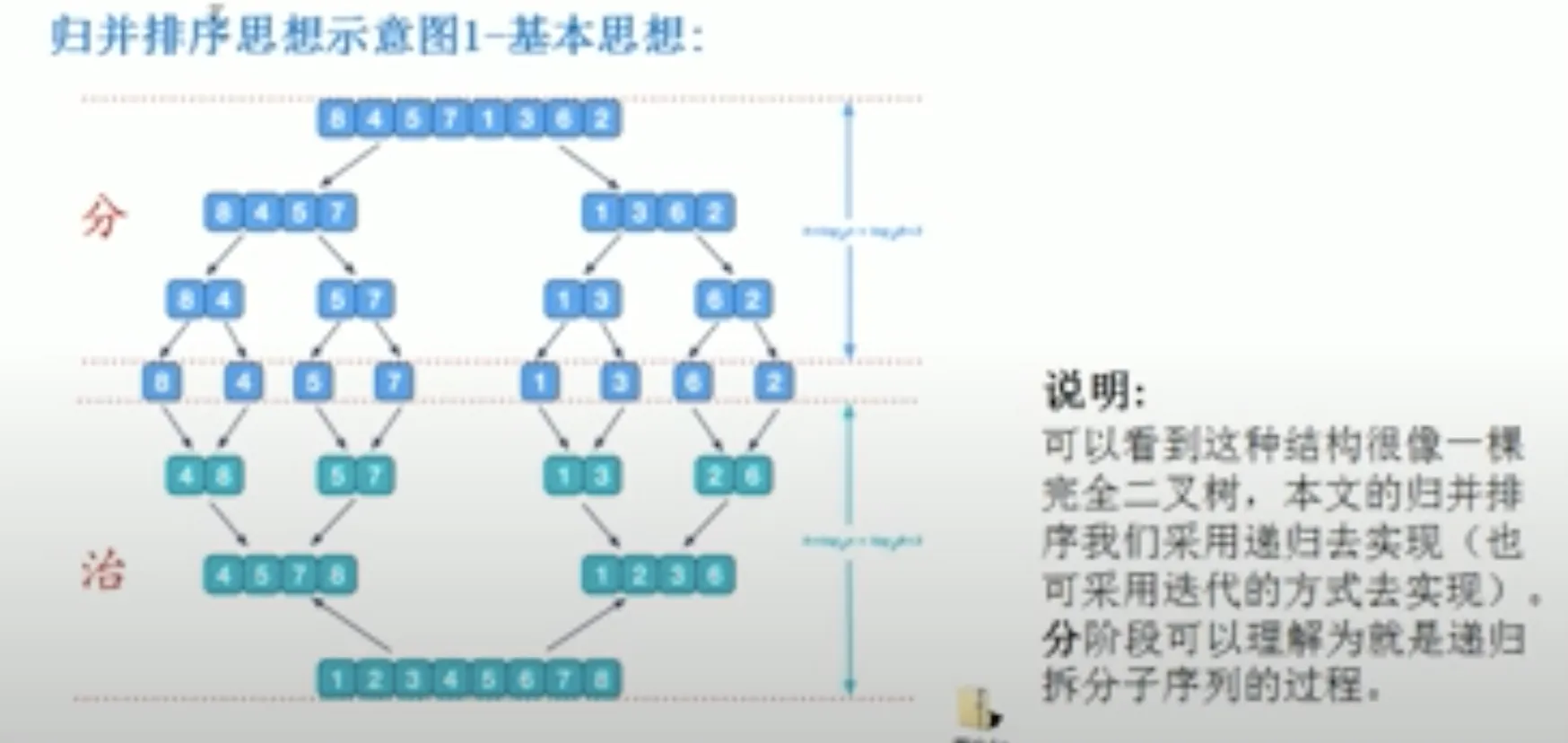

tsexport function mergeSort(arr: number[]) {
if (arr.length < 2) return arr;
const middle = arr.length >> 1;
return merge(
mergeSort(arr.slice(0, middle)),
mergeSort(arr.slice(middle))
);
function merge(lefts: number[], rights: number[]) {
let result: number[] = [];
while (lefts.length && rights.length) {
if (rights[0] < lefts[0]) {
result.push(rights.shift()!);
} else {
result.push(lefts.shift()!);
}
}
result.push(...lefts);
result.push(...rights);
return result;
}
}
快速排序
- 以第一个元素为基准,后面的数依次和它比较,最后剩下的数分成两组,一组比它大,一组比它小
- 现在就可以认为这个基准数在有序的位置了,那么他的左边和右边分别按照步骤一进行比较
- 如果数组长度为0或1就不在比较,所有分组运行完成,排序就结束了

tsexport function quickSort(arr: number[]) {
if (arr.length < 2) return arr;
const middle = arr.shift()!;
const [lefts, rights] = arr.reduce(
(sum, it) => {
if (it < middle) {
sum[0].push(it);
} else {
sum[1].push(it);
}
return sum;
},
[[], []] as [number[], number[]]
);
return [...quickSort(lefts), middle, ...quickSort(rights)];
}
快速排序优化空间复杂度
tsexport function quickSort2(
arr: number[],
left = 0,
right = arr.length - 1
) {
if (arr.length < 2) return arr;
if (left < right) {
const middle = paintion(arr, left, right);
quickSort2(arr, left, middle - 1);
quickSort2(arr, middle + 1, right);
}
return arr;
function paintion(
arr: number[],
left: number,
right: number
): number {
const piovt = left;
let index = piovt + 1;
for (let i = index; i <= right; i++) {
if (arr[i] < arr[piovt]) {
[arr[index], arr[i]] = [arr[i], arr[index]];
index++;
}
}
[arr[piovt], arr[index - 1]] = [arr[index - 1], arr[piovt]];
return index - 1;
}
}
计数排序
分布式排序使用已组织好的辅助数据结构(称为桶), 然后进行合并,得到排好序的数组。计数排序使用-一个用来存储每个元素在原始数组中出现次数的临时数组。在所有元素都计数完成后,临时数组已排好序并可迭代以构建排序后的结果数组。
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
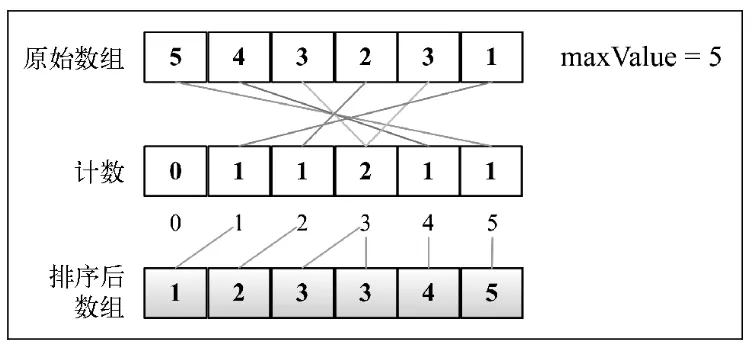
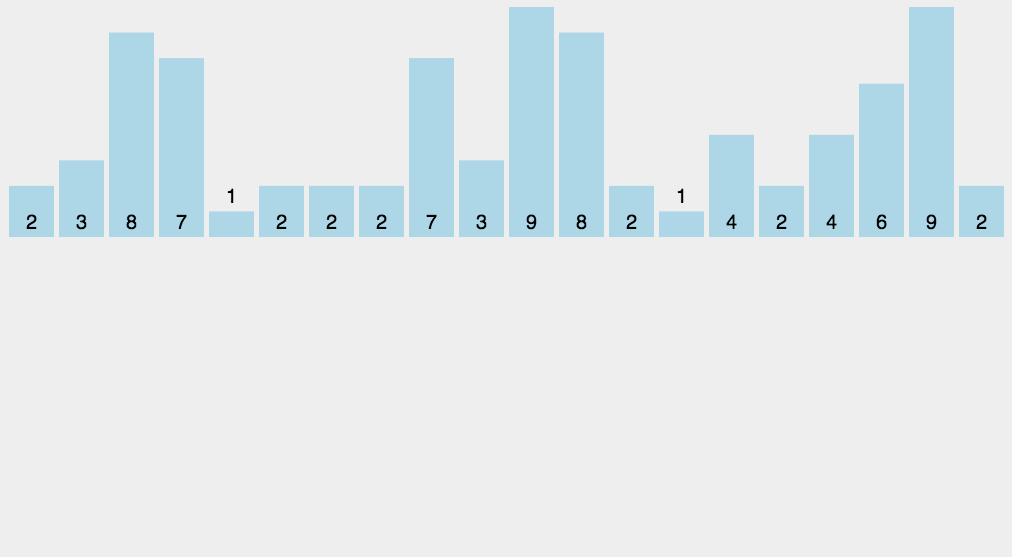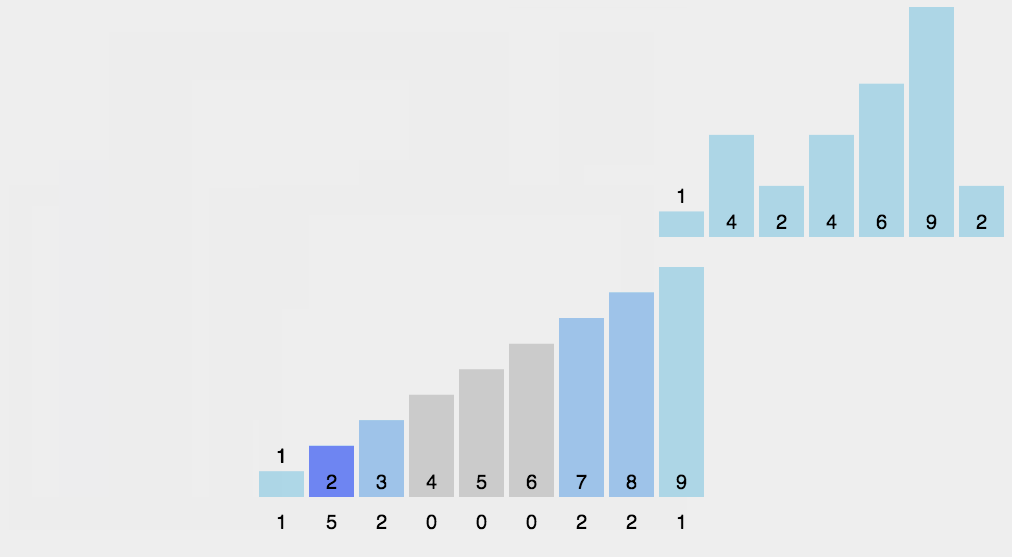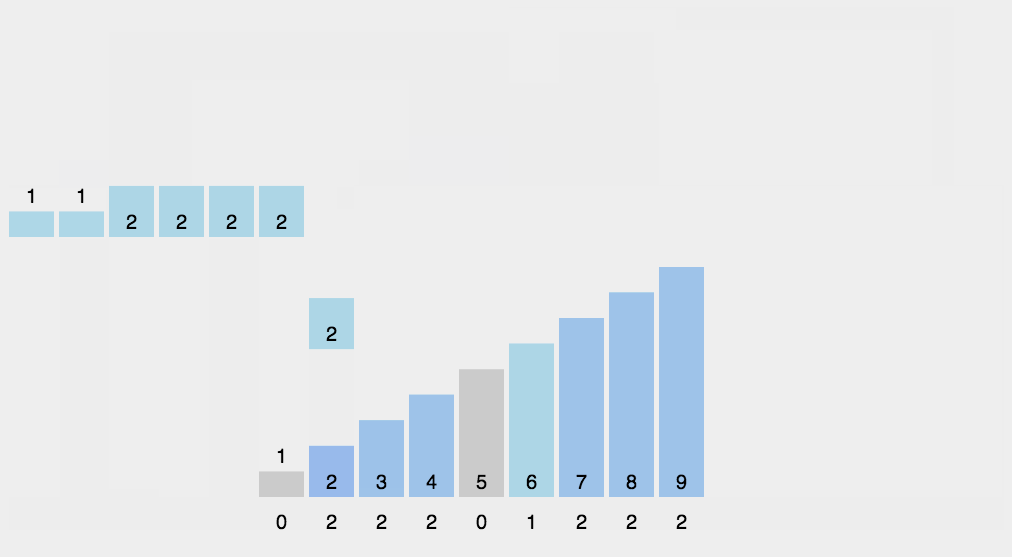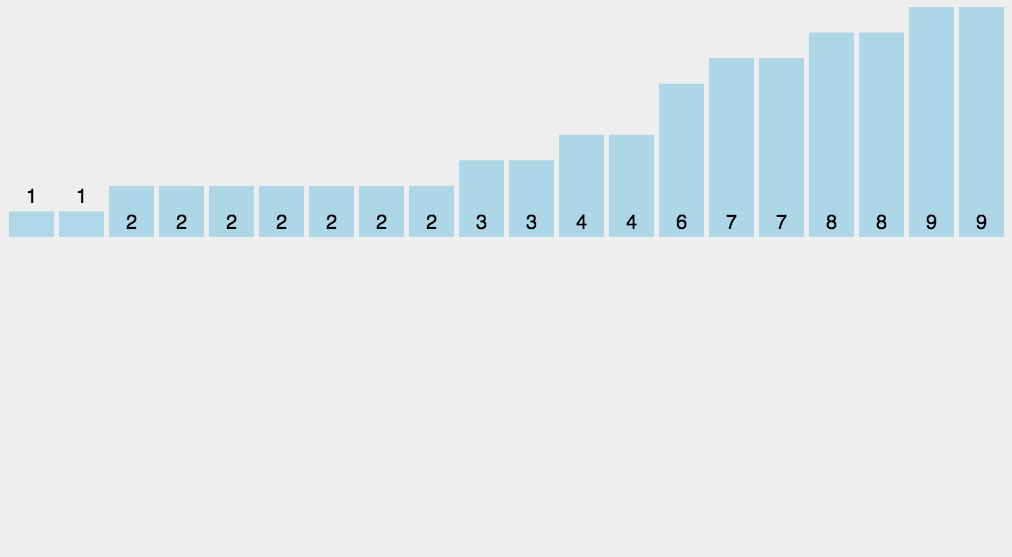
ts
export function countingSort(arr: number[]) {
if (arr.length < 2) return arr;
const obj: { [key: number]: number } = {};
arr.forEach((it, index) => {
obj[it] ??= 0;
obj[it]++;
});
return Object.keys(obj).reduce((sum, key) => {
while (obj[key]) {
sum.push(+key);
obj[key]--;
}
return sum;
}, [] as number[]);
}
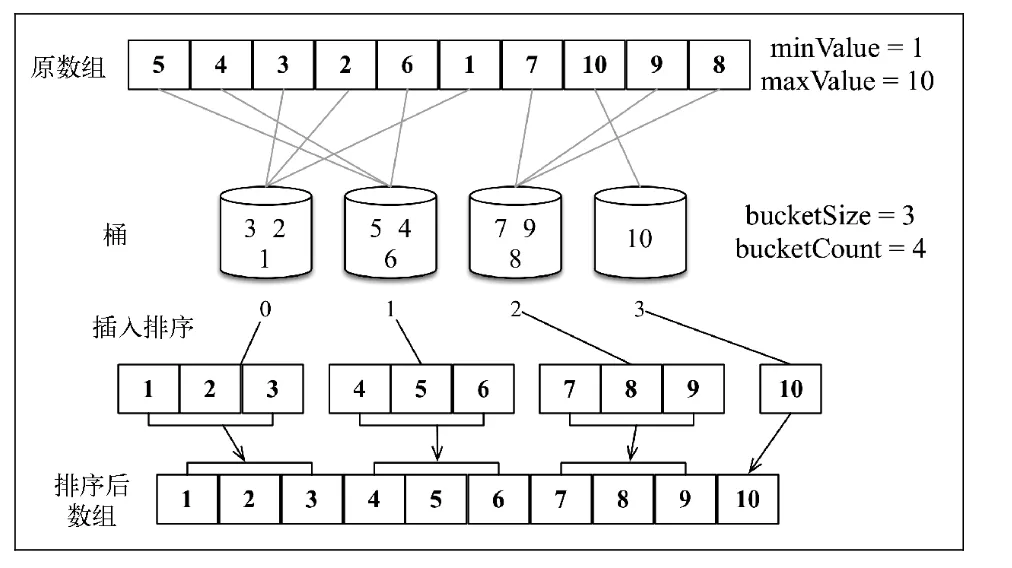
桶排序
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排)。
tsexport function bucketSort(arr: number[], bubbleSize = 5) {
if (arr.length < 2) return arr;
const [minVal, maxVal] = arr.reduce(
(sum, it) => {
if (it < sum[0]) {
sum[0] = it;
}
if (it > sum[1]) {
sum[1] = it;
}
return sum;
},
[arr[0], arr[0]]
);
const bucketCount = (maxVal - minVal) / bubbleSize + 1;
const buckets: number[][] = Array.from(
{ length: bubbleSize },
() => []
);
arr.forEach((it) => {
const index = Math.floor((it - minVal) / bucketCount);
buckets[index].push(it);
});
buckets.forEach(bubbleSort);
return buckets.flat(1);
}
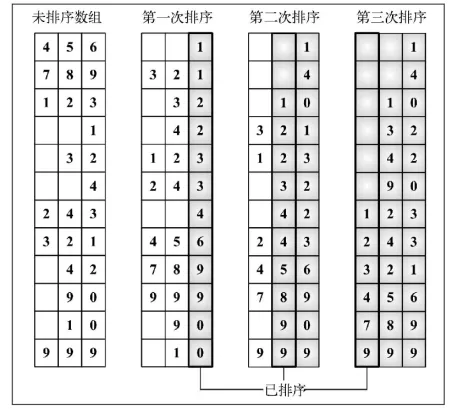
基数排序
基数排序也是-个分布式排序算法,它根据数字的有效位或基数(这也是它为什么叫基数排序)将整数分布到桶中。基数是基于数组中值的记数制的。
使用空间换时间的经典算法
tsexport function radixSort(arr: number[]) {
if (arr.length < 2) return arr;
const [minVal, maxVal] = arr.reduce(
(sum, it) => {
if (sum[0] > it) {
sum[0] = it;
}
if (sum[1] < it) {
sum[1] = it;
}
return sum;
},
[arr[0], arr[0]]
);
let diff = 0 - minVal;
const len = `${maxVal + diff}`.length;
const newArr: string[] = arr.reduce((sum, it) => {
sum.push(`${it + diff}`.padStart(len, '0'));
return sum;
}, [] as string[]);
for (let i = 0; i < len; i++) {
newArr.sort((str1, str2) => +str1[i] - +str2[i]);
}
return newArr.map((str) => +str - diff);
}
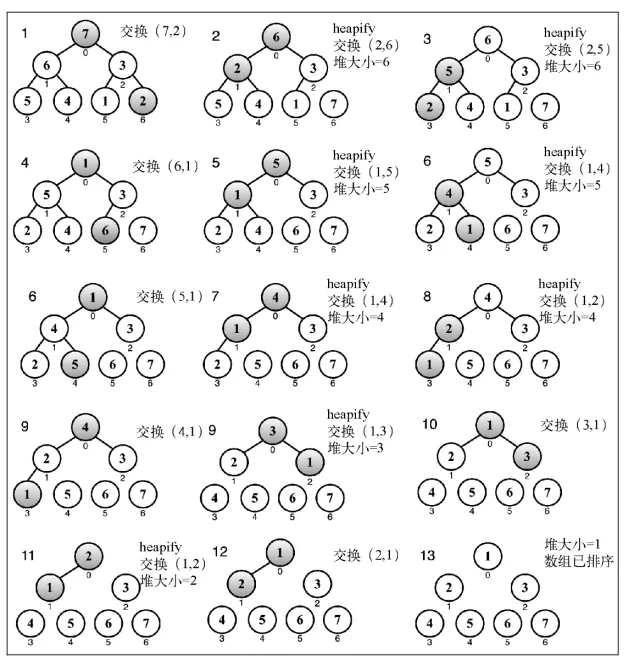
堆排序
我们可以使用二叉堆数据结构来帮助我们创建一个非常著名的排序算法:堆排序算法。它包 含下面三个步骤。
- 用数组创建一个最大堆用作源数据。
- 在创建最大堆后,最大的值会被存储在堆的第- - 个位置。我们要将它替换为堆的最后一个值,将堆的大小减1。
- 最后,我们将堆的根节点下移并重复步骤2直到堆的大小为1。
我们用最大堆得到一个升序排列的数组( 从最小到最大)。如果我们想要这个数组按降序排列,可以用最小堆代替。

ts
export function heapSort(arr: number[]) {
if (arr.length < 2) return arr;
let heapSize = arr.length;
buildMaxHeap();
while (heapSize > 1) {
--heapSize;
[arr[0], arr[heapSize]] = [arr[heapSize], arr[0]];
heapify(0, heapSize);
}
return arr;
function heapify(center: number, heapSize: number) {
const leftIndex = 2 * center + 1;
const rightIndex = 2 * center + 2;
let maxIndex = center;
if (leftIndex < heapSize && arr[maxIndex] < arr[leftIndex]) {
maxIndex = leftIndex;
}
if (rightIndex < heapSize && arr[maxIndex] < arr[rightIndex]) {
maxIndex = rightIndex;
}
if (maxIndex != center) {
[arr[maxIndex], arr[center]] = [arr[center], arr[maxIndex]];
heapify(maxIndex, heapSize);
}
}
function buildMaxHeap() {
let index = heapSize >> 1;
for (let i = index; i >= 0; i--) {
heapify(i, heapSize);
}
}
}
希尔排序
希尔排序可以说是插入排序的一种变种。无论是插入排序还是冒泡排序,如果数组的最大值刚好是在第一位,要将它挪到正确的位置就需要 n - 1 次移动。也就是说,原数组的一个元素如果距离它正确的位置很远的话,则需要与相邻元素交换很多次才能到达正确的位置,这样是相对比较花时间了。
利用二分法的思想优化插入排序
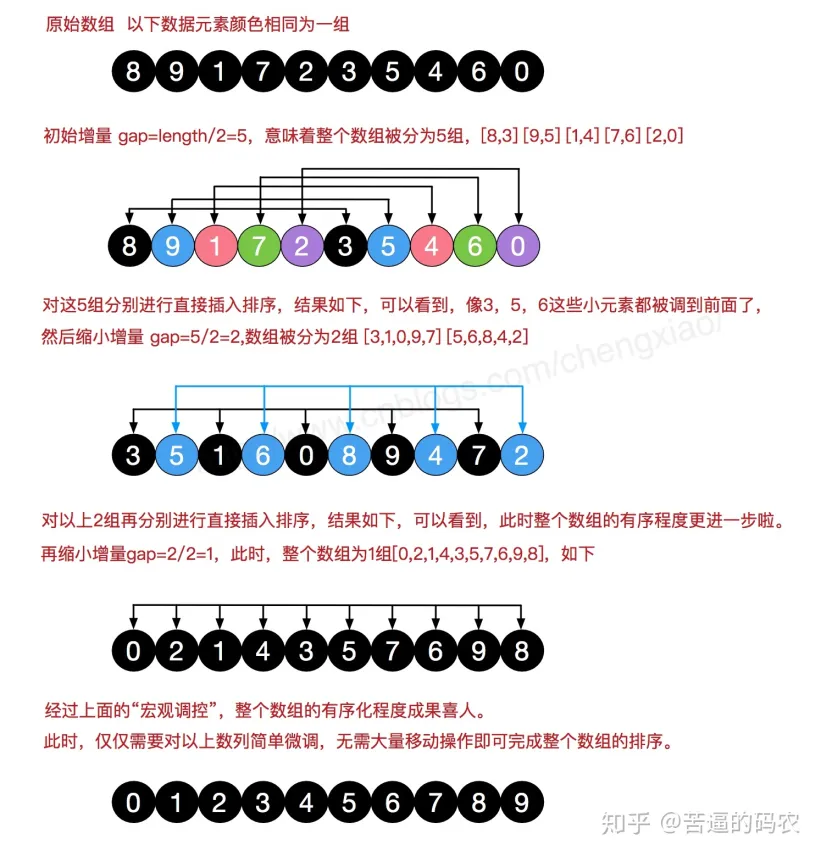

tsexport function shellSort(arr: number[]) {
let len = arr.length;
if (len < 2) return arr;
let gap = 1;
while (gap < len / 3) {
// 动态定义间隔序列
gap = gap * 3 + 1;
}
//上面是设置动态增量算法
//下面是其实是插入排序 和 冒泡排序交换位置
while (gap >= 1) {
for (let i = 0; i < len; i++) {
//插入排序
for (let j = i; j >= gap && arr[j] < arr[j - gap]; j -= gap) {
[arr[j - gap], arr[j]] = [arr[j], arr[j - gap]];
}
}
gap = (gap - 1) / 3;
}
return arr;
}
// 交换法,性能比插入排序还差
export function shellSort2(arr: number[]) {
let len = arr.length;
if (len < 2) return arr;
let count = 0; // 第几轮
for (
let gap = Math.floor(len / 2);
gap > 0;
gap = Math.floor(gap / 2)
) {
for (let i = gap; i < len; i++) {
for (let j = i - gap; j >= 0; j -= gap) {
if (arr[j] > arr[j + gap]) {
[arr[j], arr[j + gap]] = [arr[j + gap], arr[j]];
}
}
}
count++;
console.log(`第${count}轮: ${arr.join(', ')}`);
}
return arr;
}
// 移位法
export function shellSort3(arr: number[]) {
let len = arr.length;
if (len < 2) return arr;
let count = 0;
for (
let gap = Math.floor(len / 2);
gap > 0;
gap = Math.floor(gap / 2)
) {
for (let i = gap; i < len; i++) {
let j = i;
let temp = arr[j];
if (arr[j] < arr[j - gap]) {
while (j >= gap && arr[j - gap] > temp) {
arr[j] = arr[j - gap];
j -= gap;
}
arr[j] = temp;
arr[j] = temp;
}
}
count++;
// console.log(`第${count}轮: ${arr.join(', ')}`);
}
return arr;
}
算法复杂度
什么是数据结构与算法?
- 数据结构是计算机存储、组织数据的方式。
- 算法是一系列规定的计算步骤,为了实现特定的计算目的
- 程序=数据结构+算法
如何衡量算法的效率?
通常是用资源,例如CPU(时间)占用、内存(空间)占用、硬盘占用和网络占用
- 时间占比 时间复杂度 简称复杂度
- 空间占比 空间复杂度
- 时间空间复杂度 = 时间和空间增长的趋势
时间复杂度 俗称大 表示法
- 一个程序或算法的时间效率,也称“时间复杂度”,有时简称“复杂度”
- 复杂度常用大写的字母 和小写字母n来表示 , 等。n代表问题的规模
- 时间复杂度是用算法运行过程中,某个时间固定的操作需要被执行的次数和的关系来度量的。
- 在无序的列表中查找某个数,
- 最好的情况是 次,最坏的情况是 次,平均是 ,
- 通常考虑复杂度是不讨论系数的, 所以算法复杂度为
- 计算复杂度的时候,只统计执行次数最多的( 足够大时)那种固定操作的次数。比如某个算法需要执行加法 次,除法 次, 那么就计其复杂度是的。
- 复杂度有“平均复杂度”和“最坏复杂度”两种。两者可能一致,也可能不一致
- 循序查找平均复杂度和最坏复杂度一样,
- 选择冒泡插入平均复杂度和最坏复杂度都是
- 快速排序 平均复杂度是 最坏复杂度是
- 如果复杂度是多个 的函数之和,则只关心随 的增长增长得最快的那个函数。
- =>
- =>
- =>

搜索算法
常见的搜索算法有
- 顺序查找, 这个没啥好说的,算法复杂度
- 二分查找,算法复杂度
- 每次取中间数字比较大小,
- 如果中间数字大于目标值,则丢弃左边在右边查找继续执行1,反之丢弃右边,在左边查找继续执行1
- 直到找到目标数字。
- 内查搜索 对二分查找的优化,通过自适应mid从而快速找到目标值

- 举例 在
[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]中查找1 如果是二分查找需要 次,如果使用内插查找,套用上面的公式只需要 次。 - 尤其对于排列相对紧凑的数组,内插查找优势明显。
二分查找示例代码
tsexport function binarySearch(arr: number[], target: number) {
if (arr.length < 1) return -1;
if (arr[0] > target && arr.at(-1)! < target) return -1;
let left = 0;
let right = arr.length - 1;
while (left <= right) {
// console.log(Date.now());
const middle = left + ((right - left) >> 1);
if (arr[middle] === target) {
return middle;
}
if (arr[middle] > target) {
right = middle - 1;
} else {
left = middle + 1;
}
}
return -1;
}
内插查找示例代码
tsexport function interpolationSearch(arr: number[], target: number) {
if (arr.length < 1) return -1;
if (arr[0] > target && arr.at(-1)! < target) return -1;
let left = 0;
let right = arr.length - 1;
while (left <= right) {
console.log(Date.now());
const middle =
left +
((target - arr[left]) / (arr[right] - arr[left])) *
(right - left);
if (arr[middle] === target) {
return middle;
}
if (arr[middle] > target) {
right = middle - 1;
} else {
left = middle + 1;
}
}
return -1;
}
有些场景二分查找并非那么明显, 如leetcode33题 搜索旋转数组
tsfunction search(nums: number[], target: number): number {
return searchHandler(0, nums.length - 1);
function searchHandler(left: number, right: number): number {
if (left > right) return -1;
if (left === right) return nums[left] === target ? left : -1;
let middle = (left + right) >> 1;
if (nums[left] === target) return left;
if (nums[right] === target) return right;
if (nums[middle] === target) return middle;
if (nums[left] < nums[middle]) {
// 左边有序
if (target > nums[left] && target < nums[middle]) {
return searchHandler(left + 1, middle - 1);
} else {
return searchHandler(middle + 1, right - 1);
}
} else {
// 右侧有序
if (target > nums[middle] && target < nums[right]) {
return searchHandler(middle + 1, right - 1);
} else {
return searchHandler(left + 1, middle - 1);
}
}
}
}
JavaScript算法优化技巧
递归优化
递归很消耗性能因为要保存所有调用栈中的信息,举个例子
jsfunction Fibonacci (n) {
if ( n <= 1 ) {return 1};
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
// console.log(Fibonacci(10)) // 约1s
// console.log(Fibonacci(40)) // 约1s
// console.log(Fibonacci(45)) // 约10-15s
// console.log(Fibonacci(50)) // 卡死
解决方式是使用尾调用优化
tsfunction Fibonnacci2(n, ac1 = 1, ac2 = 1) {
if(n ===1) return ac2;
return Fibonnacci2(n-1, ac2, ac1+ac2);
}
console.log(Fibonnacci2(1000)); // <1s响应
上述代码改变了函数的参数,可以使用柯里化优化代码
tsfunction currying(fn, ...rest) {
return function(...args) {
return fn.call(this, ...args, ...rest);
}
}
const Fibonnacci3 = currying(Fibonnacci2, 1, 1);
console.log(Fibonnacci3(50)) // ok
总结: 尾调用解决函数调用过程中由于需要所有保存调用栈信息占用太多内存,导致运算速度变慢的问题。
调用栈溢出问题
JS引擎对JS函数调用栈有限制,如果超出最大栈调用深度会报错
举个例子
jsfunction sum(n) {
if (n === 1) return 1;
return 1 + sum(n - 1);
}
console.log(sum(10469)); // ok
console.log(sum(10470)); // 刚好栈溢出
// RangeError: Maximum call stack size exceeded
解决该问题的思路是 用循环代替递归
jsfunction trampline(f) {
while(f instanceof Function) {
f = f();
}
return f;
}
function mySum(x, y) {
if(y>0) {
return mySum.bind(null, x+1,y-1)
} else {
return x;
}
}
console.log(trampline(mySum(0, 10470))); // ok
console.log(trampline(mySum(0, 104700))); // ok
蹦床函数并不是真正的尾递归优化,下面的实现才是
jsfunction tco(fn) {
let active = false
const accumulator = [];
let result;
return function() {
accumulator.push(arguments)
if(!active) {
active = true;
while(accumulator.length) {
result = fn.apply(this, accumulator.shift());
}
active = false;
return result
}
}
}
const sum2 = tco(function(x, y) {
if(y>0) {
return sum2(x+1,y-1)
} else {
return x;
}
})
console.log(sum2(0, 104700))
分治算法
分而治之是算法设计中的一种方法,它将原问题分解为多个和原问题相似的小问题,递归解决小问题,再将解决方式合并以解决原来的问题
分治算法可以分为三个部分
- 分解原问题为多个子问题
- 解决子问题,用返回子问题的方式的递归算法
- 组合这些子问题的解决方式,得到原问题的解
分治算法可以求解一些经典问题
- 二分搜索
- 大整数乘法
- 棋盘算法
- 归并排序
- 快速排序
- 线性时间选择
- 最接近点对问题
- 循环赛日程表
- 汉诺塔
汉诺塔代码实现
jsfunction hannuoTower(num, a, b, c) {
if (num === 1) return console.log(`把${a}盘移动到${c}盘`);
// 1、把最上面的盘从A盘移动到B盘, 会使用到C盘
hannuoTower(num - 1, a, c, b);
// 2、 把最下面的盘 A移动到C
console.log(`把${a}盘移动到${c}盘\n`);
// 3、 把B上面的所有盘移动到C盘
hannuoTower(num - 1, b, a, c);
}
hannuoTower(5, 'A', 'B', 'C');
贪心算法
贪心算法遵循一种近似解决问题的技术。期待通过每个阶段的局部最优选择,从而达到全局最优解
贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解),但是都是相对近似(接近)最优解的结果
集合覆盖问题
假设存在下面需要付费的广播台,以及广播台信息可以覆盖的地区,如何选择最少多少个广播台,让所有的地区都可以接收到信号
| 广播台 | 覆盖地区 |
|---|---|
| K1 | 北京、上海、天津 |
| K2 | 广州、北京、深圳 |
| K3 | 成都、上海、杭州 |
| K4 | 上海、天津 |
| K5 | 杭州、大连 |
tsvar map = new Map();
map.set('k1', ['北京', '上海', '天津']);
map.set('k2', ['广州', '北京', '深圳']);
map.set('k3', ['成都', '上海', '杭州']);
map.set('k4', ['上海', '天津']);
map.set('k5', ['杭州', '大连']);
console.log(getMinLeitai(map).join(', '));
function getMinLeitai(boardcasts: Map<string, Array<string>>) {
const allAreas = new Set();
[...boardcasts.keys()].forEach((key) => {
boardcasts.get(key)!.forEach((item) => allAreas.add(item));
});
const selects: string[] = [];
let tempArr: string[] = [];
let maxKey: string | null = null;
while (allAreas.size > 0) {
maxKey = null;
for (const item of boardcasts) {
tempArr = item[1].filter((val) => allAreas.has(val));
if (
tempArr.length &&
(maxKey === null ||
boardcasts.get(maxKey)!.length < tempArr.length)
) {
maxKey = item[0];
}
}
if (maxKey !== null) {
selects.push(maxKey);
boardcasts.get(maxKey)!.forEach((val) => allAreas.delete(val));
}
}
return selects;
}
最少硬币找零
tsfunction minCoinChange(coins: number[], amount: number) {
const change: number[] = [];
let total = 0;
coins.sort((a, b) => b - a); // 贪心算法体现
for (let i = 0; i < coins.length; i++) {
const coin = coins[i];
while (total + coin <= amount) {
change.push(coin);
total += coin;
}
}
return change;
}
console.log(minCoinChange([1, 2, 10, 5], 26).join(', '));
总的来说 贪心算法比较简单,这里不在举例
回溯算法
回溯是一种渐进式寻找并构建问题解决方式的策略。我们从一个可能的动作开始并试着用这个动作解决问题。如果不能解决,就回溯并选择另-个动作直到将问题解决。根据这种行为,回溯算法会尝试所有可能的动作(如果更快找到了解决办法就尝试较少的次数)来解决问题。
有一些可用回溯解决的著名问题:
- 骑士巡逻问题.
- N皇后问题
- 迷宫老鼠问题
- 数独解题器
骑士周游


测试用例
tsimport { describe, expect, test } from 'vitest';
import { horseTreads } from '../ts_algorithm/backtrack';
describe('test 马踏棋盘', () => {
test('3 * 4的棋盘,起点00', () => {
const chessBorads = horseTreads(3, 4, 0, 0);
expect(chessBorads).toEqual([
[1, 8, 3],
[4, 11, 6],
[7, 2, 9],
[10, 5, 12],
]);
});
});
ts// X、Y表示棋盘X轴、Y轴大小 ,x、y 表示马儿起始位置所在X、Y轴的坐标
export function horseTreads(
X: number,
Y: number,
x: number,
y: number
): number[][] {
const visited = Array.from({ length: X * Y }, () => false);
const chessBorads: number[][] = Array.from(
{
length: Y,
},
() => Array.from({ length: X })
);
let finished = false;
return traversalChessBoards(x, y);
function traversalChessBoards(
x: number,
y: number,
step = 1
): number[][] {
visited[y * X + x] = true;
chessBorads[y][x] = step;
// ...
const nexts = getNextStep({ x, y });
// 下一步最少的是最优解,
// 这里是贪心算法,当然不要这一步也可以通过
nexts.sort(
(a, b) => getNextStep(b).length - getNextStep(a).length
);
while (nexts.length) {
const next = nexts.pop()!;
if (!visited[next.y * X + next.x]) {
traversalChessBoards(next.x, next.y, step + 1);
}
}
if (step < X * Y) {
if (!finished) {
visited[y * X + x] = false;
chessBorads[y][x] = 0;
}
} else {
finished = true;
}
return chessBorads;
}
function getNextStep(currPoint: { x: number; y: number }) {
const nextSteps: Array<{ x: number; y: number }> = [];
let y: number, x: number;
// 这里的位置看前面的图
// 0
if ((x = currPoint.x + 2) < X && (y = currPoint.y - 1) >= 0) {
nextSteps.push({ y, x });
}
// 1
if ((x = currPoint.x + 2) < X && (y = currPoint.y + 1) < Y) {
nextSteps.push({ y, x });
}
// 2
if ((x = currPoint.x + 1) < X && (y = currPoint.y + 2) < Y) {
nextSteps.push({ y, x });
}
// 3
if ((x = currPoint.x - 1) >= 0 && (y = currPoint.y + 2) < Y) {
nextSteps.push({ y, x });
}
// 4
if ((x = currPoint.x - 2) >= 0 && (y = currPoint.y + 1) < Y) {
nextSteps.push({ y, x });
}
// 5
if ((x = currPoint.x - 2) >= 0 && (y = currPoint.y - 1) >= 0) {
nextSteps.push({ y, x });
}
// 6
if ((x = currPoint.x - 1) >= 0 && (y = currPoint.y - 2) >= 0) {
nextSteps.push({ y, x });
}
// 7
if ((x = currPoint.x + 1) < X && (y = currPoint.y - 2) >= 0) {
nextSteps.push({ y, x });
}
return nextSteps;
}
}
老鼠迷宫
测试用例
tsdescribe('test 马踏棋盘', () => {
test('3 * 4的棋盘,起点00', () => {
const chessBorads = ratInAMaze([
[1, 0, 0, 0],
[1, 1, 1, 1],
[0, 0, 1, 0],
[0, 1, 1, 1],
]);
expect(chessBorads).toEqual([
[1, 0, 0, 0],
[1, 1, 1, 0],
[0, 0, 1, 0],
[0, 0, 1, 1],
]);
});
});
代码实现
tsexport function ratInAMaze(maze: (0 | 1)[][]): Array<Array<0 | 1>> {
const solution: Array<Array<0 | 1>> = Array.from(
{ length: maze.length },
() => Array.from({ length: maze[0].length }, () => 0)
);
let hasSolution = false;
step(0, 0);
return solution;
function step(i: number, j: number) {
if (i >= maze.length || j >= maze[0].length) return false;
if (!maze[i][j]) {
return false;
}
if (i == maze.length - 1 && j == maze[0].length - 1) {
solution[i][j] = 1;
hasSolution = true;
return true;
}
solution[i][j] = 1;
if (step(i + 1, j)) {
return true;
}
if (step(i, j + 1)) {
return true;
}
solution[i][j] = 0;
return false;
}
}
复原 IP
- 给定一个只包含数字的字符串,复原它并返回所有可能的 IP 地址格式。
- 有效的 IP 地址正好由四个整数(每个整数位于 0 到 255 之间组成),整数之间用 '.' 分隔。
测试用例
tstest('test IP复原', () => {
const realIp = restoreIP('25525511135');
expect(realIp).toEqual('255.255.11.135');
});
代码实现
tsexport function restoreIP(ip: string): string {
// 假设这个ip有解,先不校验它
// 可能有多个解 只要求出一个即可(回溯算法的本质)
const solutions: string[] = [];
run(ip);
return solutions.join('.');
function run(rest: string, step = 1): boolean {
if (rest === '' && step === 5) {
return true;
}
if (!(step < 5 && rest)) return false;
const nexts = getNext(rest);
for (const one of nexts) {
solutions.push(one);
if (run(rest.substring(one.length), step + 1)) {
return true;
}
solutions.pop();
}
return false;
}
function getNext(rest: string): string[] {
let results: string[] = [];
results.push(rest[0]);
if (rest[1] && +rest[0] < 3) {
results.push(rest.substring(0, 2));
if (rest[2] && +rest[1] < 6) {
results.push(rest.substring(0, 3));
}
}
results.reverse(); // 贪心优化
return results;
}
}
回溯算法题
- leetcode 40题 组合之和 回溯 + 剪枝
- leetcode 37题 解数独 回溯+ 状态压缩
- leetcode 46题 全排列
动态规划
动态规划( dynamic programming, DP )是一种将复杂问题分解成更小的子问题来解决的优化技术。
注意,动态规划和分而治之是不同的方法。
- 分而治之方法是把问题分解成相互独立的子问题,然后组合它们的答案,
- 而动态规划则是将问题分解成相互依赖的子问题。
用动态规划解决问题时,要遵循三个重要步骤:
- 定义子问题;
- 实现要反复执行来解决子问题的部分(递归);
- 识别并求解出基线条件。
能用动态规划解决的一些著名问题如下。
- 背包问题:给出一组项,各自有值和容量,目标是找出总值最大的项的集合。这个问题的限制是,总容量必须小于等于“背包”的容量。
- 最长公共子序列:找出一组序列的最长公共子序列(可由另一序列删除元素但不改变余下元素的顺序而得到)。
- 矩阵链相乘:给出一系列矩阵,目标是找到这些矩阵相乘的最高效办法( 计算次数尽可能少)。相乘运算不会进行,解决方案是找到这些矩阵各自相乘的顺序。
- 硬币找零:给出面额为d, ... , 的一定数量的硬币和要找零的钱数,找出有多少种找零的方法。
- 图的全源最短路径: 修路问题
Floyd-Warshall算法
背包问题
问题描述
与一个背包,容量为4,现有以下物品
| 物品 | 重量 | 价格 |
|---|---|---|
| 吉他(G) | 1 | 1500 |
| 音响(S) | 4 | 3000 |
| 电脑(L ) | 3 | 2000 |
- 要求达到的目标为装入的背包的总价值最大,并且重量不超出
- 要求装入的物品不能重复
思路分析和图解
算法的主要思想, 利用动态规划来解决。每次遍历到的第i个物品,根据w[i]和v[i]来确定是否需要将该物品放入背包中。即对于给定的n个物品,设v[i]、 w[i]分别为第i个物品的价值和重量,C为背包的容量。再令v[i][j]表示在前i个物品中能够装入容量为j的背包中的最大价值。则我们有下面的结果:
| 物品i / 容量j | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 吉他(G) | 0 | 1500G | 1500G | 1500G | 1500G |
| 音响(S) | 0 | 1500G | 1500G | 1500G | 3000S |
| 电脑(L ) | 0 | 1500G | 1500G | 2000L | 2000L+1500G |
v[i][0] = v[0][j]// 表示填入表的第一行第一列是0- 当
w[i] > j时;v[i][j] = v[i-1][j]// 当准备加入新增的商品容量大于当前背包的容量时,就直接使用上一个单元格的装入策略 - 当
j>=w[i]时;v[i][j] = max(v[i-1][j] , v[i]+v[i-1][j-w[i]])
当准备加入新增的商品容量不大于当前背包的容量时,装入的方式:
v[i-1][j]上一个单元格装入的最大值v[i]当前商品的价值v[i-1][j-w[i]]装入i-1商品,搭配剩余空间j-w[i]的最大值
代码实现
tsvar map = new Map();
map.set('G', [1, 1500]);
map.set('S', [4, 3000]);
map.set('L', [3, 2000]);
console.log(getMaxValOnDiffGoods(map, 4));
function getMaxValOnDiffGoods(map: Map<string, [number, number]>, size) {
const dp = Array.from({ length: map.size + 1 }, () =>
Array.from({ length: size + 1 }, () => 0)
);
/* const path = Array.from({ length: size + 1 }, () =>
Array.from({ length: size + 1 }, () => 0)
);
const goods = [...map.keys()]; */
const [w, val] = [...map.values()].reduce(
(sum, it) => {
sum[0].push(it[0]);
sum[1].push(it[1]);
return sum;
},
[[], []] as [number[], number[]]
);
let maxVal = 0;
console.log('start');
// dp[i][j] 把前i个物品装入容量为j的背包
for (let i = 1; i < dp.length; i++) {
for (let j = 1; j < dp[i].length; j++) {
if (j < w[i - 1]) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.max(dp[i - 1][j], val[i - 1] + dp[i - 1][j - w[i - 1]]);
maxVal = Math.max(dp[i][j], maxVal);
}
}
}
return maxVal;
}
最长公共子序列
tsconst str1 = 'acecd';
const str2 = 'acded';
console.log(getMaxCommonSeq(str1, str2));
function getMaxCommonSeq(str1: string, str2: string) {
const dp = Array.from({ length: str1.length + 1 }, () =>
Array.from(
{
length: str2.length + 1,
},
() => 0
)
);
let maxLen = 0;
// dp[i][j] 表示 字符串 `0-i` 与字符串 `0-j` 的最长公共子序列
for (let i = 1; i < dp.length; i++) {
for (let j = 1; j < dp[i].length; j++) {
if (str1[i - 1] === str2[j - 1]) {
dp[i][j] = Math.max(dp[i][j - 1], 1 + dp[i - 1][j - 1]);
} else {
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
maxLen = Math.max(maxLen, dp[i][j]);
}
}
return maxLen;
}
更多动态规划算法
- 爬楼梯
- leetcode第5题 最长回文字符串
- vue3 DomDiff 最大上升子序列
- leetcode 第42题 接水滴
- Floy算法
这里 是我的leetcode刷题记录
本文作者:郭郭同学
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!